In Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
To find the area of the shaded region in the given figure, we will follow these steps:
Step 1: Identify the components of the figure
In the figure, we have:
- A quadrant of a circle with radius r=14 cm.
- A semicircle with diameter BC.
Step 2: Calculate the length of BC
Using the Pythagorean theorem in triangle ABC:
BC2=AB2+AC2
Since AB=AC=14 cm, we have:
BC2=142+142=196+196=392
Thus,
BC=√392=14√2 cm
Step 3: Find the radius of the semicircle
The radius of the semicircle BXC is half of BC:
Radius of semicircle=BC2=14√22=7√2 cm
Step 4: Calculate the area of the semicircle
The area Asemicircle is given by:
Asemicircle=12πr2=12π(7√2)2=12π(49⋅2)=12π⋅98=49π cm2
Step 5: Calculate the area of the quadrant
The area Aquadrant of the quadrant BAC is given by:
Aquadrant=90360πr2=14π(14)2=14π⋅196=49π cm2
Step 6: Calculate the area of triangle ABC
The area Atriangle of triangle ABC is given by:
Atriangle=12×AB×AC=12×14×14=98 cm2
Step 7: Calculate the area of the shaded region
The area of the shaded region is given by:
Ashaded=Asemicircle−(Aquadrant−Atriangle)
Substituting the values:
Ashaded=49π−(49π−98)=98 cm2
Final Answer
The area of the shaded region is 98 cm2.
---
In the figure, we have:
- A quadrant of a circle with radius r=14 cm.
- A semicircle with diameter BC.
Using the Pythagorean theorem in triangle ABC:
BC2=AB2+AC2
Since AB=AC=14 cm, we have:
BC2=142+142=196+196=392
Thus,
BC=√392=14√2 cm
The radius of the semicircle BXC is half of BC:
Radius of semicircle=BC2=14√22=7√2 cm
The area Asemicircle is given by:
Asemicircle=12πr2=12π(7√2)2=12π(49⋅2)=12π⋅98=49π cm2
The area Aquadrant of the quadrant BAC is given by:
Aquadrant=90360πr2=14π(14)2=14π⋅196=49π cm2
The area Atriangle of triangle ABC is given by:
Atriangle=12×AB×AC=12×14×14=98 cm2
The area of the shaded region is given by:
Ashaded=Asemicircle−(Aquadrant−Atriangle)
Substituting the values:
Ashaded=49π−(49π−98)=98 cm2
The area of the shaded region is 98 cm2.
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Exercise 12.214videos
AREAS RELATED TO CIRCLES
- BOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE 12.15videos
AREAS RELATED TO CIRCLES
- BOOK - NCERT ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - All Questions65videos
ARITHMETIC PROGRESSIONS
Similar Questions
ABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
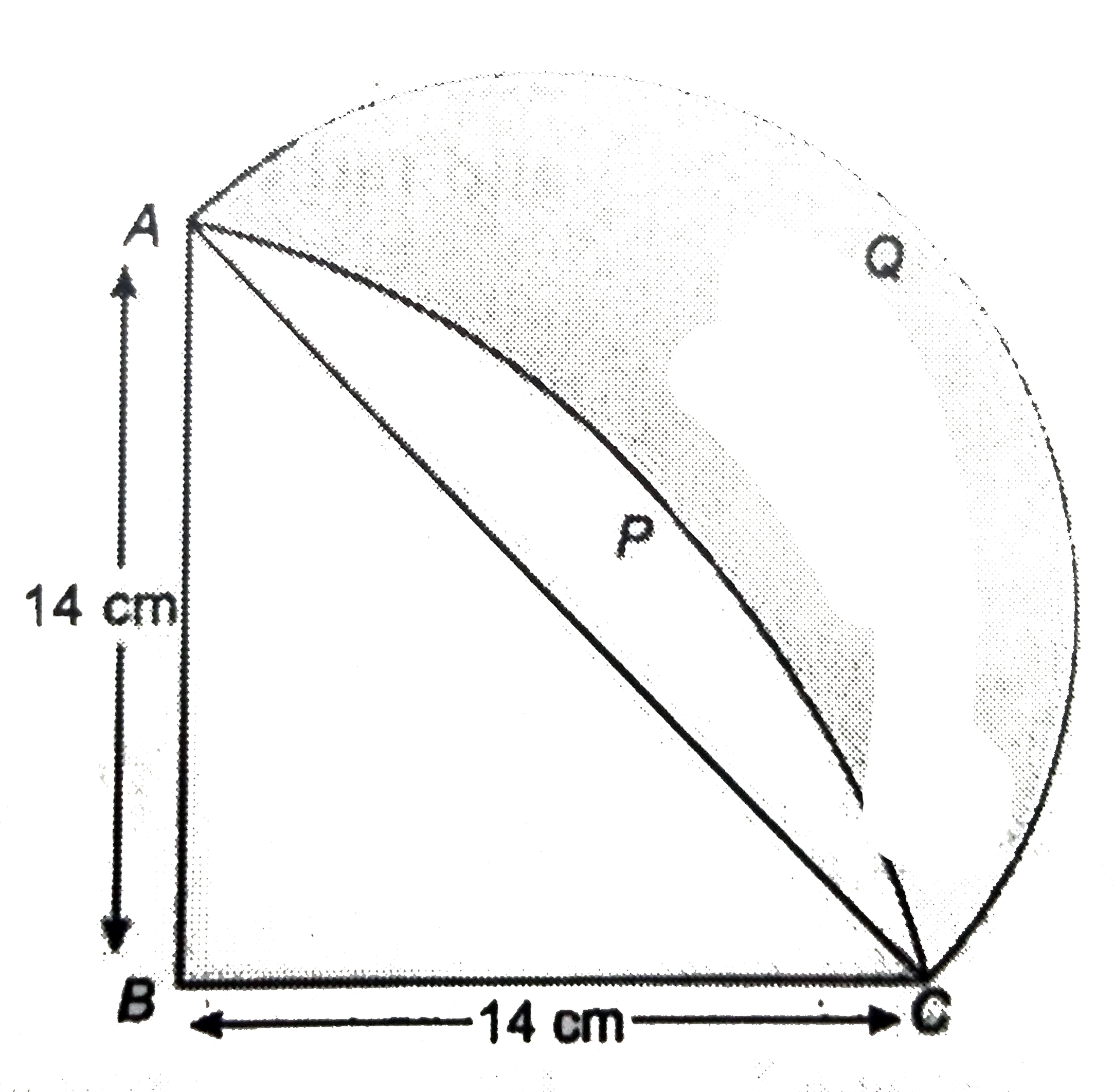 View Solution
View SolutionABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionFind the area of a quadrant of a circle whose radius is 14 cm.
View SolutionIn the given figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semi circles are drawn with AD and BC as diameters. Find the area of the shaded region
(Take π=227)
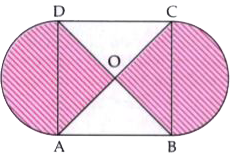 View Solution
View SolutionPQRS is a diameter of a circle of radius 6 cm. The length PQ, QR and RS are equal Semicircle are drawn on PQ and QS as diameters. Find the area of the shaded region. Find also the length of boundaries of shaded portion.
View SolutionIn Figure-9, a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, Find the area of the shaded region.
View SolutionIn Figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O . Find the area of the shaded region.
View SolutionThree semicircles each of diameter 3 cm, a circle of diameter 4·5 cm and a semicircle of radius 4·5 cm are drawn in the given figure. Find the area of the shaded region.
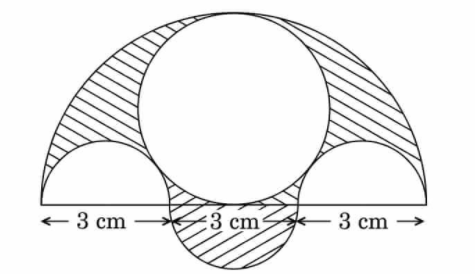 View Solution
View SolutionThree semicircles each of diameter 3 cm, a circle of diameter 4·5 cm and a semicircle of radius 4·5 cm are drawn in the given figure. Find the area of the shaded region.
 View Solution
View SolutionThree semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the adjoining figure. Find the area of the shaded region.
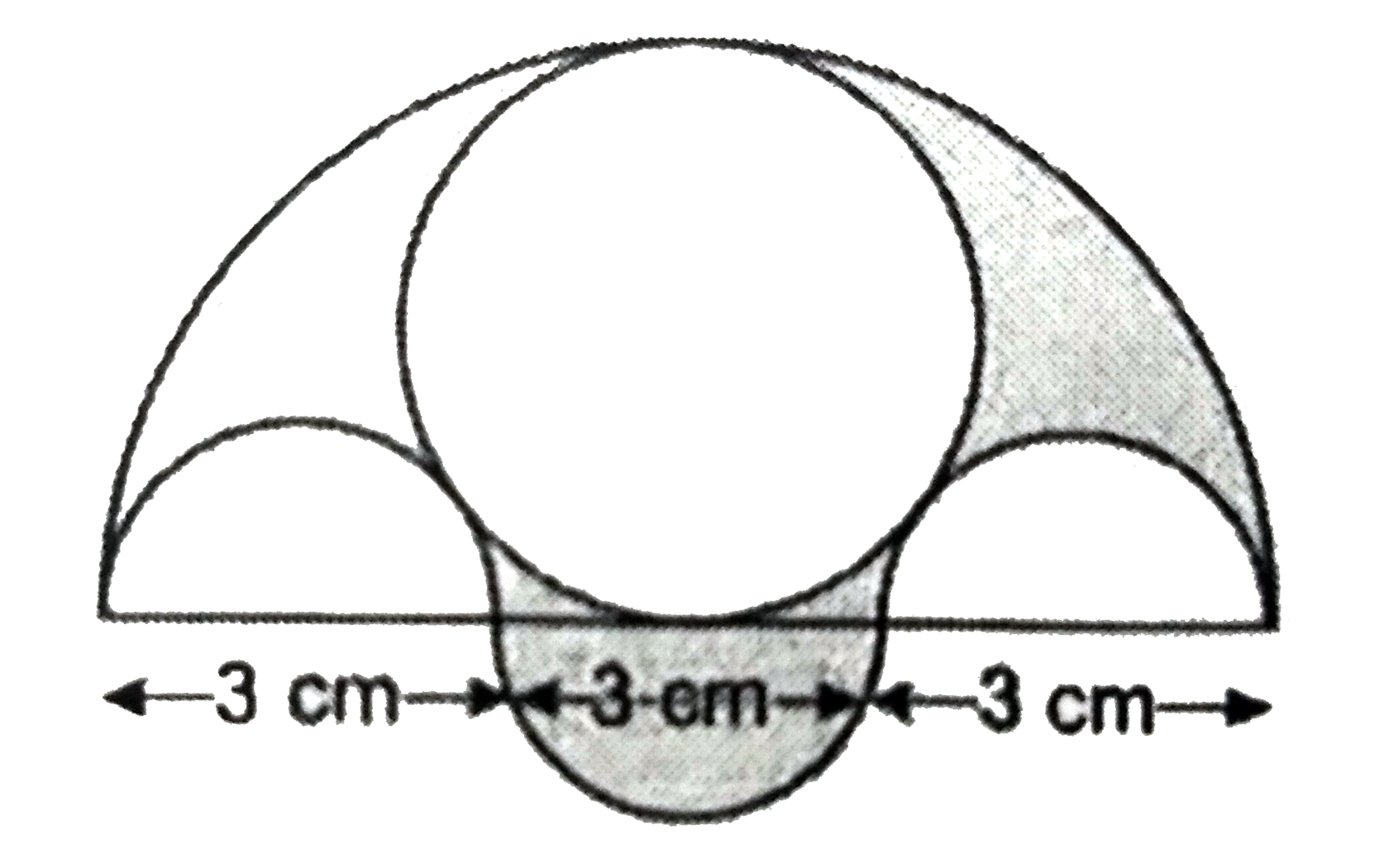 View Solution
View Solution

