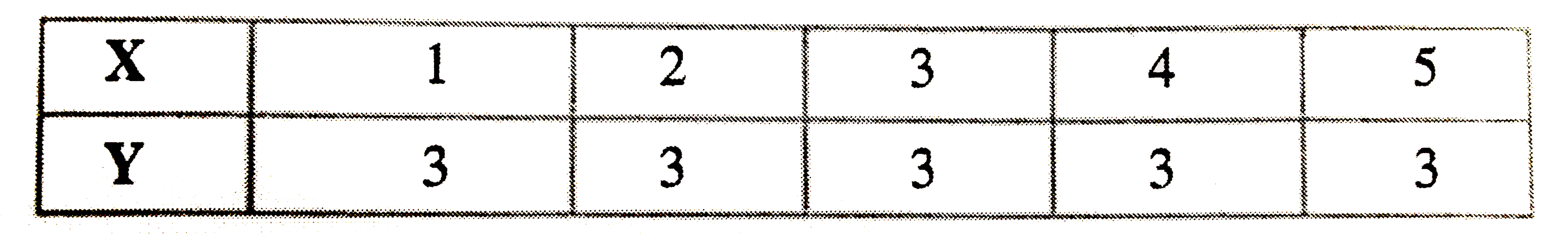The two variates X and Y are such that (X+Y) is always equal to 100. Therefore the correlation is perfect and positive.
To determine whether the statement "The two variates X and Y are such that (X + Y) is always equal to 100. Therefore the correlation is perfect and positive" is true or false, we can follow these steps:
Step 1: Understand the relationship between X and Y
Given that X+Y=100, we can express Y in terms of X:
Y=100−X
Step 2: Analyze the equation
The equation Y=100−X is a linear equation. This indicates that there is a linear relationship between X and Y.
Step 3: Determine the slope of the line
The slope of the line represented by the equation Y=100−X is -1. This means that for every unit increase in X, Y decreases by 1 unit.
Step 4: Identify the regression coefficient
The regression coefficient of Y on X (denoted as bYX) is equal to the slope of the regression line. Therefore:
bYX=−1
Step 5: Relate regression coefficient to correlation coefficient
The sign of the regression coefficient indicates the direction of the correlation. Since the regression coefficient bYX is -1, it implies that the correlation coefficient r will also be negative:
r=−1
Step 6: Conclusion
Since the correlation coefficient is -1, it indicates a perfect negative correlation between X and Y. Therefore, the statement that the correlation is perfect and positive is false.
Final Answer
The statement is false.
---
Given that X+Y=100, we can express Y in terms of X:
Y=100−X
The equation Y=100−X is a linear equation. This indicates that there is a linear relationship between X and Y.
The slope of the line represented by the equation Y=100−X is -1. This means that for every unit increase in X, Y decreases by 1 unit.
The regression coefficient of Y on X (denoted as bYX) is equal to the slope of the regression line. Therefore:
bYX=−1
The sign of the regression coefficient indicates the direction of the correlation. Since the regression coefficient bYX is -1, it implies that the correlation coefficient r will also be negative:
r=−1
Since the correlation coefficient is -1, it indicates a perfect negative correlation between X and Y. Therefore, the statement that the correlation is perfect and positive is false.
The statement is false.
Topper's Solved these Questions
- CORRELATION AND REGRESSION BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - QUESTION (STATE GIVING REASONS, WHETHER EACH OF THE FOLLOWING STATEMENTS IS TRUE OR FALSE)
10 Videos
- CORRELATION AND REGRESSION BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - PROBLEM SET (1) (MCQ)
37 Videos
- CORRELATION AND REGRESSION BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - QUESTION (FILL IN THE BLANKS)
13 Videos
- CONCEPTS OF SET THEORY BOOK - ML KHANNACHAPTER - CONCEPTS OF SET THEORY EXERCISE - Self Assessment Test
13 Videos
- DEFINITE INTEGRALBOOK - ML KHANNACHAPTER - DEFINITE INTEGRALEXERCISE - Miscellaneous Questions (Assertion/Reason)
1 Videos
Similar Questions
Knowledge Check
If X and Y are two sets, then X∩(Y∩X)'equals
AXBYCϕDNone of theseif X and Y are two sets , then X∩(Y∪X)'equals
AXBYCϕDnone of theseConsider the following statements:
1. Two independent variables are always uncorrelated.
2. The coefficient of correlation between two variables X and Y is positive when X decreases then Y decreases. Which of the above statements is/are correct?A1 onlyB2 onlyCBoth 1 and 2DNeither 1 nor 2
Let X and Y be two variables with correlation coefficient e. If the values of X and Y serires and changed such that the cov (X,Y) remains unchanged while the variance of X and Y becomes 4 times their original values, then find the new correlation coefficient between X and Y.
View SolutionIf two variables X and Y are connected by the relation 2x+y=3, then e(x,y) is equal to
View SolutionThe two variates X and Y are uncorrelated and have standard deviations σXandσY respectively, the correlation coefficient between X+Y and X−Y is
View SolutionIf two variables X and Y are independent, then what is correlation coefficient between them
View Solutionif X and Y are two sets , then X∩(Y∪X)'equals
View Solution