Let N be the set of natural number and R be the relation in N×N defined by : (a,b) R (c,d) iff ad = bc, for all (a,b), (c,d) ∈N×N Show that R is an equivalence relation.Solution in Punjabi
Step by step video & image solution for Let N be the set of natural number and R be the relation in NxxN defined by : (a,b) R (c,d) iff ad = bc, for all (a,b), (c,d) in NxxN Show that R is an equivalence relation. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RELATIONS AND FUNCTIONBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONEXERCISE - EXAMPLE
212 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EXERCISE
543 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXAMPLE
13 Videos
Similar Questions
Which one of the following graph represents the function of x? Why?
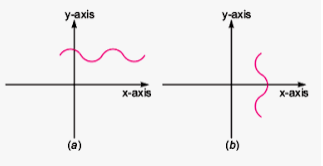
View SolutionCompute P(A∣B),if P(B)=0.5 and P(A∩B)=0.32
View SolutionState the reason for the relation R, in the set {1,2,3} given by R= {(1,2), (2, 1), not to be transitive.
View SolutionLet R be a relation over the set NxxN and it is defined by (a,b)R(c,d)impliesa+d=b+c . Then R is
View SolutionN प्राकृतिक संख्याओं का समुच्चय है, सम्बन्ध R समुच्चय N×N पर इस प्रकार परिभाषित है कि
.(a,b)R(c,d)⇔ad=bc
सिद्ध कीजिए कि R एक तुल्यता सम्बन्ध है । समुच्चय N×N के दो अवयव बताइए जिनका सम्बन्ध (1,2) से है ।
View Solutionमाना N प्रकृत संख्याओं का समुच्य है तथा (a,b)R(c,d) यदि और केवल यदि ad(b+c)=bc(a+d)
जांच कीजिय की R,N×N में तुल्यता सम्बन्ध है या नहीं |
View Solutionमाना N सही प्रकृत संख्याओं का समुछ्य है और R,N×N पर सम्बन्ध है तथा इस प्रकार परिभाषित है --- (a,b)R(c,d)⇔ad=bc
दर्शाइए की R एक तुल्यता सम्बन्ध है |
View SolutionLet NN be the set of natural numbers and R be a relation on NN×NN defined by,
(a,b) R (c,d) → a+d=b+c, for all (a,b) and (c,d) iNNN×NN.
prove that R is an equivalence relation on NN×NN.
View SolutionLet N N be the set of natural numbers and R be a relation on N NxxN N defined by, (a,b) R (c,d) to ad =bc , for all (a,b) and (c,d) iN N NxxN N . Show that R is an equivalence relation on N NxxN N .
View SolutionLet N denote the set of all natural numbers and R be the relation on N×N defined by (a,b)R (c,d) if ad(b+c)=bc(a+d) then R is
View SolutionLet R be a relation on N×N defined by (a,b) R(c,d)⇔a+d=b+c if (a,b),(c,d)∈N×N then show that: (i) (a,b)R (a,b) for all (a,b)∈N×N (ii) (a,b)R(c,d)⇒(c,d)R(a,b)for all (a,b), (c,d)∈N×N (iii) (a,b)R (c,d)and (c,d)R(e,f)⇒(a,b)R(e,f) for all (a,b), (c,d), (e,f)∈N×N
View SolutionProve that the relation R on the set N×N defined by (a, b)R (c, d)⇔a+d=b+c for all (a, b), (c, d)∈N×N is an equivalence relation. Also, find the equivalence classes [(2, 3)] and [(1, 3)].
View SolutionLet N be the set of all natural numbers and let R be a relation on N×N , defined by (a, b)R (c, d)⇔ad=bc for all (a, b), (c, d)∈N×N . Show that R is an equivalence relation on N×N
View SolutionIf R is a relation on N×N defined by (a,b) R (c,d) iff a+d=b+c, then
View SolutionIf N denotes the set of all natural numbers and R be the relation on N×N defined by (a, b) R (c, d) if ad(b+c)=bc(a+d). Show that R is an equivalence relation.
View SolutionIs R an equivalence relation in the set N×N which is defined as (i) (a,b)R(c,d)⇔a+d=b+c (ii) (a,b)R(c,d)⇔ad=bc for all (a,b),(c,d)∈N×N?
View Solution
