If the operation ⊕ is defined by a ⊕b=a2+b2 for all real numbers 'a' and 'b', then (2⊕3)⊕4 is Solution in Punjabi
181
182
184
185
Step by step video & image solution for If the operation o+ is defined by a o+ b = a^2 + b^2 for all real numbers 'a' and 'b', then (2o+3)o+4 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RELATIONS AND FUNCTIONBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONEXERCISE - EXAMPLE
212 Videos
- PROBABILITYBOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EXERCISE
543 Videos
- RELATIONS AND FUNCTIONSBOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXAMPLE
13 Videos
Similar Questions
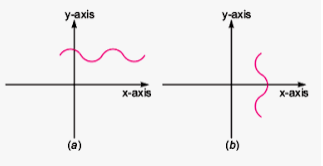
Which one of the following graph represents the function of x? Why?
View SolutionCompute P(A∣B),if P(B)=0.5 and P(A∩B)=0.32
View SolutionState the reason for the relation R, in the set {1,2,3} given by R= {(1,2), (2, 1), not to be transitive.
View SolutionQ+ denote the set of all positive rational numbers. If the binary operation ⊙ on Q+ is defined as a ⊙b=ab2, then the inverse of 3 is 43 (b) 2 (c) 13 (d) 23
View Solution'o' on N defined by a o b= a b + b a for all a, b∈N define a binary operation on the given set or not:
View Solutionमाना कि ⊕ तथा ⊕, N पर, a⊕b=2a तथा a⊕b=2ab द्वारा परिभाषित है। निर्धारित करें कि ये द्विआधारी संक्रियाएँ हैं या नहीं
View Solutionपूर्णांक संख्याओं पर एक फलन इस प्रकार परिभाषित है कि aob=a−b | क्या O एक द्विचर संक्रिया है ।
View SolutionLet A be the set of all real numbers except -1 and an operation 'o' be defined on A by aob = a+b + ab for all a, b∈A, then identify elements w.r.t. 'o' is
View Solutionवास्तविक संख्याओं के समुच्चय में दो द्विचर संक्रियाएँ ∗ और ⊙ निम्न जैसा परिभाषित है :
a∗b=a−b और a⊙B=ab.
सिद्ध करें कि संक्रिया ∗,⊙ पर बंटनीय नहीं है ।
View Solutionif the operation ⊙ is defined for all real numbers a and b by the relation ⊙=a2b3
then 2 ⊙{3⊙(−1)}
View SolutionDefine group.Show that under the binary operation O defined on Q+ by aob=ab2 is a group.
View SolutionLet * be a binary operation o Q defined by a*b= ab4 for all a,b∈ Q ,find identity element in Q
View SolutionDetermine whether O on Z defined by a O b=ab for all a, b∈Z define a binary operation on the given set or not:
View Solution'o' on N defined by a o b= a b + b a for all a, b∈N define a binary operation on the given set or not:
View SolutionLet A be the set of all real numbers except -1 and an operation 'o' be defined on A by aob = a+b + ab for all a, b∈A, then identify elements w.r.t. 'o' is
View Solution
