Take a piece of thread. Tie a small stone at one end. Hold the other end of the thread and whirl it round as shown. Note the motion of the stone.
Release the thread. Again note the direction of motion of the stone.
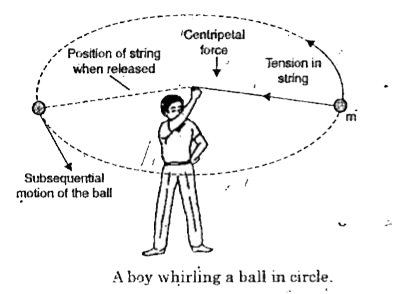
Before releasing the thread, the stone moves in a circular path with a constant speed, and change in plirection at every point. The change in direction involves change in velocity or acceleration. The force that attracts this acceleration and keeps the body moving along the circular path, acts towards the centre. This force is called centripetal force.
When the thread, is released i.e., in the absence centripetal force, the stone flies off along the straight line. This straight line will be tangent to the circle.
Topper's Solved these Questions
- GRAVITATIONBOOK - NAND LAL PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Intext Questions
11 Videos
- GRAVITATIONBOOK - NAND LAL PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - Exercises
27 Videos
- FORCE AND LAWS OF MOTIONBOOK - NAND LAL PUBLICATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - Additional Questions (Short Answer Questions)
8 Videos
- MOTIONBOOK - NAND LAL PUBLICATIONCHAPTER - MOTIONEXERCISE - ADDITIONAL QUESTIONS (Short Answer Type Question)
1 Videos
Similar Questions
Take a piece of thread. Tie a small piece of stone to one end of the thread. Hold the other end of the thread in hand and whirl it round. Note the motion of the stone. If the thread breakes suddenly, the stone files off along tangent to the circle at the instant.
Read the above passage and answer the following question:
(i) which force is whirling the stone ? who is providing this force ?
(ii) why does the stone fly off along the tangnet to the circle at that instant?
(iii) what value of life do you learn from this?
View SolutionA stone is attached to one end of a string and rotated in a vertical circle . If the string breaks at the position of maximum tension , then it will break at
View Solution
Knowledge Check
IF a stone is tied to one end of the string and whirled in verticle circle, then the tension in the string at the lowest point is equal to
Acentripetal forceBthe difference between centripetal force and weight of the stoneCthe addition of the centripetal force and weight of the stoneDweight of the stoneA stone is fastened to one end of a string and is whirled in a verticla circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
Av=√3RgBv=√RgCv=√4RgDv=√7RgA stone tied to one end of rope and rotated in a circular motion . If the string suddenly breaks then the stone travels.
Ain perpedicular directionBin direction of centrfugal forceCtowards centripetal forceDin tangential direction
A stone tied to a string is rotated in a circle. If the string is cut, the stone flies away from the circle because
View SolutionA stone tied at the end of sring is whirled in a circle. If the string break , the stone flies away tangentially . Why ?
View SolutionA stone tied to a string is rotated in a circle. If the string is cut, the stone flies away from the circle because
View SolutionA stone tied to the end of the string 100 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 30 revolution in 15 s. Calculate the magnitude and direction of acceleration of the stone.
View SolutionA stone is fastened to one end of a string and is whirled in a verticla circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
View Solution
