If A = diag (d1,d2,d3,….dn) then det A is equal to Solution in Punjabi
0
d1+d2+d3….+dn
d1d2d3….dn
None of these
Step by step video & image solution for If A = diag (d_1,d_2,d_3,….d_n) then det A is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DETERMINANTSBOOK - PRADEEP PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - EXERCISE
342 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - PRADEEP PUBLICATIONCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - EXERCISE
788 Videos
- DIFFERENTIAL EQUATIONSBOOK - PRADEEP PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE
507 Videos
Similar Questions
If A=[13−10787], write the following submatrices of A. A12
View SolutionExamine the continuity of f(x)={x2−9x−3x≠36x=3 at x = 3
View SolutionDetermine the order and the degree of each of the following equations. Also state if these are linear or non-linear.
(xy2+x)dx+(y−x2y)dy=0
View SolutionIf D=diag(d1,d2,d3,…,dn) where d≠0 for all I=1,2,…,n, then D−1is equal to
View SolutionIn the following circuit of PN junction diodes D_1, D_2 and D_3 are ideal then i is
View SolutionIfD=diag[d1,d2,dn] , then prove that f(D)=diag[f(d1),f(d2),,f(dn)],wheref(x) is a polynomial with scalar coefficient.
View SolutionIfD=diag[d1,d2,dn] , then prove that f(D)=diag[f(d1),f(d2),,f(dn)],wheref(x) is a polynomial with scalar coefficient.
View Solutionin the foll. Circuit of PN junction , diodes D1,D2andD3 are ideal then I is
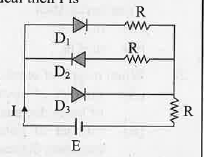
View SolutionIf d1,d2,d3 be the three distinct diagonals of a regular octagon, such that d1<d2<d3, find the ratio of the inradius to the circumradius of the octagon.
View Solutionfour fair dice D1,D2,D3andD4 each having six faces numbered 1,2,3,4,5 and 6 are rolled simultaneously. The probability that D4 shows a number appearing on one of D1,D2,D3 is
View SolutionIf D=diag(d1,d2,d3,…,dn) where d≠0 for all I=1,2,…,n, then D−1is equal to
View SolutionIf D=diag(d1,d2,d3,…,dn) where d≠0 for all I=1,2,…,n, then D−1is equal to
View SolutionStatement 1: if D=diag[d1,d2,,dn],then D−1=diag[d−11,d−12,...,d−1n] Statement 2: if D=diag[d1,d2,,dn],then Dn=diag[dn1,dn2,...,dnn]
View SolutionIfD=diag[d1,d2,dn] , then prove that f(D)=diag[f(d1),f(d2),,f(dn)],wheref(x) is a polynomial with scalar coefficient.
View Solutionfour fair dice D1,D2,D3andD4 each having six faces numbered 1,2,3,4,5 and 6 are rolled simultaneously. The probability that D4 shows a number appearing on one of D1,D2,D3 is
View Solutionfour fair dice D1,D2,D3andD4 each having six faces numbered 1,2,3,4,5 and 6 are rolled simultaneously. The probability that D4 shows a number appearing on one of D1,D2,D3 is
View Solution
