Calculate the void space in fcc packing of n spheres of radius 1 nm, n spheres of radius 0.414 nm, and 2n spheres of radius 0.225 nm in appropriate voids.Solution in Malayalam
0.19
0.26
0.17
0.12
The correct Answer is:A
Consider unit cell of fcc, volume occupied by spheres
=(4×43π×13)+4×43π(0.414)3+8×43π(0.225)3=18.32cm3
Edge length a=4r√2=4√2
Volume of cube=(4√2)3=22.627
Packing fraction=18.3222.627=0.8096=80.96%
It is clear from the figure that the arrangement is sc, with coordination number (CN) of each point=6.
(The arrangement shown in figure consists of 4 unit cells. taking a view of one unit cell, the atoms are occupied at corners and face centres of each unit cell).
Topper's Solved these Questions
- SOLID STATEBOOK - BRILLIANT PUBLICATIONCHAPTER - SOLID STATEEXERCISE - LEVEL-3 (Multiple Correct Answer Type)
13 Videos
- SOLID STATEBOOK - BRILLIANT PUBLICATIONCHAPTER - SOLID STATEEXERCISE - LEVEL-3 (Matching Column Type)
5 Videos
- SOLID STATEBOOK - BRILLIANT PUBLICATIONCHAPTER - SOLID STATEEXERCISE - LEVEL-2
46 Videos
- REDOX REACTION & ELECTROCHEMISTRYBOOK - BRILLIANT PUBLICATIONCHAPTER - REDOX REACTION & ELECTROCHEMISTRYEXERCISE - QUESTION (ELECTROCHEMISTRY) (LEVEL -II) (ASSERTION-REASON)
3 Videos
- SOLUTIONSBOOK - BRILLIANT PUBLICATIONCHAPTER - SOLUTIONSEXERCISE - Level-III (Linked Comprehension Type)
12 Videos
Similar Questions
Which of the following statements are correct ?
View SolutionMatch the crystal systems/unit cells mentioned in Column I with their characteristic features mentioned in Column II.
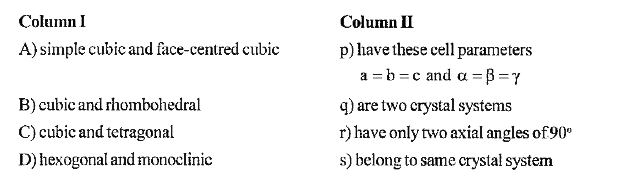
View SolutionIn NaCl type structure, if all ions along an axis joining centres of the opposite face centers are missing, the expression for packing fraction in limiting case is:
View SolutionAssertion: After the electrolysis of aqueous CuSO4 solution pH decreases.
Reason: Sulphuric acid is formed.
View Solution1 mole of A and 1 mole B are mixed together to form an ideal solution at 25∘C. Solution is placed in a vessel fitted with piston. If pressure on the solution is reduced isothermally.
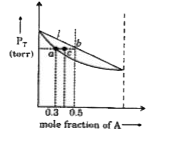
Correct relationship between P∘AandP∘B is
View SolutionCalculate the void space in closest packing of n spheres of radius 1 unit, n spheres of radiys 0.414 units, and 2n spheres of radius 0.225 units.
View SolutionIf in a closest packed arrangement r is the radius of the sphere respresenting the tetrahedral void and R is the radius of the spheres in closest packed arrangement then
View SolutionAssertion:A tetrahedral void is surrounded by four spheres and an octahedral void is surrounded by six spheres.
Reason:The number of tetrahedral voids is double the number of close packed spheres and number of octahedral voids is equal to number of close packed spheres.
View SolutionFind the size of largest sphere that will fit in octahedral void in an ideal FCC crystal as a function of atomic radius 'r'. The insertion of this sphere into void does not distort the FCC lattice. Calculate the packing fraction of FCC lattice when all the octahedral voids are filled by this sphere.
View SolutionFind the size of largest sphere that will fit in octahedral void in an ideal FCC crystal as a function of atomic radius 'r'. The insertion of this sphere into void does not distort the FCC lattice. Calculate the packing fraction of FCC lattice when all the octahedral voids are filled by this sphere.
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
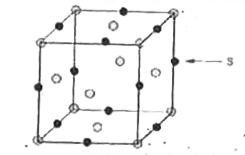
In the figure given below, the site marked as S is a
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound is
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In Schottky defect
View SolutionAssertion:A tetrahedral void is surrounded by four spheres and an octahedral void is surrounded by six spheres.
Reason:The number of tetrahedral voids is double the number of close packed spheres and number of octahedral voids is equal to number of close packed spheres.
View SolutionIn a close-packed structure, if r is the radius of the spherical void and R is the radius of the spheres forming voids, the critical r/R value for the tetrahedral void is equal to
View Solution
