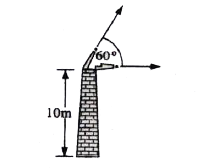
Two canons intalled at the top of a cliff 10 m high fire a shot each with speed $5 \sqrt{3}$ m/s at some interval. One canon fires at $60^{\circ}$ with the horizontal whereas the second fires horizontally. The coordinates of the point of collision of the shots are

$3 \sqrt{5} m, 3 m$

$\frac{1}{5 \sqrt{3}} m, \frac{1}{5} m$

$\frac{1}{3} m, \frac{1}{3 \sqrt{5}} m$

$5 \sqrt{3} m, 5 m$

Text Solution

Verified by Experts

The correct Answer is:D

$x = (5 \sqrt{3} cos 60) t_{1} = 5 \sqrt{3} t_{2}, y = 10 + 5 \sqrt{3} sin 60, t_{1} - \frac{1}{2} g t_{1}^{2} = 10 - \frac{1}{2} g t_{2}^{2}$
Solving $t_{1} = 2 s and t_{2} = 1 s, x = 5 \sqrt{3}, y = 5 m$

Class 11 PHYSICS PROJECTILE MOTION

Knowledge Check

From the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of $20 {m s}^{- 1}$ The horizontal range of the projectile is
A $10 \sqrt{3}$
B20 m
C $20 \sqrt{3} m$
D $40 \sqrt{3}$

Two guns situated at the top of a hill of height $10 m$ fire one shot each with the same speed $5 \sqrt{3} m / s$ at some interval of time. One gun fires horizontal and the other fores upwards at an angle of $60^{\circ}$ with the horizontal. Two shots collide in air at a poit $P$ . Find (i) time-interval between the firing and (ii) coordinates of the point $P$ . Take the origin of coordinates system at the foot of the hill right below the muzzle and trajectorise in the $x - y$ plane.
View Solution
Two guns situated at the top of a hill of height $10 m$ fire one shot each with the same speed $5 \sqrt{3} m / s$ at some interval of time. One gun fires horizontal and the other fores upwards at an angle of $60^{\circ}$ with the horizontal. Two shots collide in air at a poit $P$ . Find (i) time-interval between the firing and (ii) coordinates of the point $P$ . Take the origin of coordinates system at the foot of the hill right below the muzzle and trajectorise in the $x - y$ plane.
View Solution
Two guns are situated at the top of a hill firing the shots at the same speed. One gun fires the shot horizontally and other gun fires the shot at an angle of $60^{\circ}$ with horizontal. Two two shots collide in air. If the time taken by horizontal shot to reach the point of collision in $3 sec o n d s$ , find the time interval between two shots.
View Solution
Two guns are situated at the top of a hill firing the shots at the same speed. One gun fires the shot horizontally and other gun fires the shot at an angle of $60^{\circ}$ with horizontal. Two two shots collide in air. If the time taken by horizontal shot to reach the point of collision in $3 sec o n d s$ , find the time interval between two shots.
View Solution
From the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of $20 {m s}^{- 1}$ The horizontal range of the projectile is
View Solution
A projectile is fired form the top of a 40 m high cliff with an initial speed of 50 m/s at an unknown angle. Find its speed when it hits the ground.
View Solution
Two persons simutaneously aim and fire their guns at a bird sitting on a tree. The first person fires his shot with a speed of $100 m / s$ at an angle of projection of $30^{\circ}$ . The second person is ahead of the first by a distance of $50 m$ and fire his shot with a speed of $80 m / s$ . how must he aim his gun so that both the shots hit the bird simultaneously. Calculate the distance of the foot of the frre from two persons and the height of the tree. With what velocities and when do the two shorts hit the bird.
View Solution

Two canons intalled at the top of a cliff 10 m high fire a shot each with speed $5 \sqrt{3}$ m/s at some interval. One canon fires at $60^{\circ}$ with the horizontal whereas the second fires horizontally. The coordinates of the point of collision of the shots are

The correct Answer is:D

$x = (5 \sqrt{3} cos 60) t_{1} = 5 \sqrt{3} t_{2}, y = 10 + 5 \sqrt{3} sin 60, t_{1} - \frac{1}{2} g t_{1}^{2} = 10 - \frac{1}{2} g t_{2}^{2}$
Solving $t_{1} = 2 s and t_{2} = 1 s, x = 5 \sqrt{3}, y = 5 m$

Similar Questions

Knowledge Check

From the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of $20 {m s}^{- 1}$ The horizontal range of the projectile is

Recommended Questions

Two canons intalled at the top of a cliff 10 m high fire a shot each with speed 5√3 m/s at some interval. One canon fires at 60∘ with the horizontal whereas the second fires horizontally. The coordinates of the point of collision of the shots are

The correct Answer is:D

x=(5√3cos60)t1=5√3t2, y=10+5√3sin60, t1−12gt21=10−12gt22 Solving t1=2sandt2=1s, x=5√3, y=5m

Similar Questions

Knowledge Check

From the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of 20 m s−1 The horizontal range of the projectile is

Recommended Questions

Two canons intalled at the top of a cliff 10 m high fire a shot each with speed $5 \sqrt{3}$ m/s at some interval. One canon fires at $60^{\circ}$ with the horizontal whereas the second fires horizontally. The coordinates of the point of collision of the shots are

$x = (5 \sqrt{3} cos 60) t_{1} = 5 \sqrt{3} t_{2}, y = 10 + 5 \sqrt{3} sin 60, t_{1} - \frac{1}{2} g t_{1}^{2} = 10 - \frac{1}{2} g t_{2}^{2}$
Solving $t_{1} = 2 s and t_{2} = 1 s, x = 5 \sqrt{3}, y = 5 m$

From the ground, a projectile is fired at an angle of 60 degree to the horizontal with a speed of $20 {m s}^{- 1}$ The horizontal range of the projectile is