If in ΔABC,AB=AC (see figure), BP and CQ be the altitudes from the vertices to their opposite sides, then
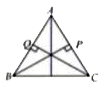
BP=CQ
AP=AQ
∠ABC=∠ACB
All of these
The correct Answer is:D
Step by step video, text & image solution for If in DeltaABC, AB=AC (see figure), BP and CQ be the altitudes from the vertices to their opposite sides, then by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-2 )
10 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Multiple Choice Questions) (MATCH THE FOLLOWING)
2 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.5)
4 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
Knowledge Check
In ΔABC,P,Q,R are the feet of angle bisectors from the vertices to their opposite sides as shown in the figure. ΔPQR is constructed
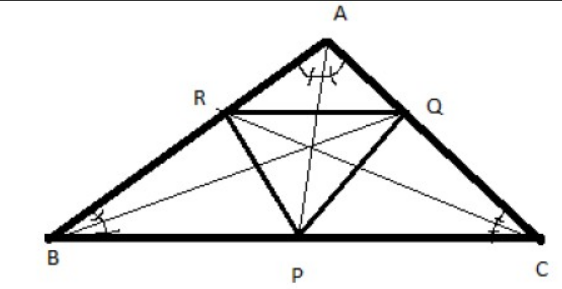
If AB=7 units, BC = 8 units, AC = 5 units, then the side PQ will beA√283 unitsB√883 unitsC√783 unitsD√843 unitsIn ΔABC,P,Q,R are the feet of angle bisectors from the vertices to their opposite sides as shown in the figure. ΔPQR is constructed

If ∠BAC=120∘, then measusred of ∠RPQ will beA60∘B90∘C120∘D150∘If in a !ABC , the altitudes from the vertices A , B , C on the opposite sides are in H.P., then sin A, sin B , sin C are in
AH.P.BAGPCA.P.DG.P.
If ΔABC is an isosceles triangle with AB = AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionIf ABC is an isosceles triangle with AB=AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionIf ABC is an isosceles triangle with AB=AC . Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionIf in a !ABC , the altitudes from the vertices A , B , C on the opposite sides are in H.P., then sin A, sin B , sin C are in
View SolutionIn ΔABC, if AB=ACandBD=DC (see figure), then ∠ADC=
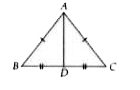
View Solution
