ABCD is a square and ABE is an equilateral triangle outside the square then
∠ACE=12∠ABE
∠ACE=∠ABE
∠ACE=2∠ABE
None of these
The correct Answer is:A
To solve the problem involving the square ABCD and the equilateral triangle ABE, we will follow these steps:
Step 1: Understanding the Shapes
We have a square ABCD and an equilateral triangle ABE constructed outside the square.
Step 2: Identify the Properties of the Shapes
1. In a square, all sides are equal and all angles are 90 degrees.
2. In an equilateral triangle, all sides are equal and all angles are 60 degrees.
Step 3: Assigning Angles
- Let’s denote the angles of triangle ABE:
- Angle ABE = 60 degrees
- Angle BAE = 60 degrees
- Angle AEB = 60 degrees
Step 4: Finding the Angles of the Square
- Since ABCD is a square:
- Angle ABC = 90 degrees
- Angle BCD = 90 degrees
- Angle CDA = 90 degrees
- Angle DAB = 90 degrees
Step 5: Relationship Between the Angles
- Since ABE is an equilateral triangle, we have:
- AB = BE (sides of the equilateral triangle)
- Since ABCD is a square, we have:
- AB = BC (sides of the square)
Step 6: Conclusion
From the above relationships, we can conclude:
- Since AB = BE and AB = BC, it follows that BC = BE.
- Therefore, triangle ABE is congruent to triangle ABC in terms of side lengths.
Step 7: Finding Angle AEC
To find angle AEC, we can use the property of angles in a triangle:
- Since angle ABE = 60 degrees and angle ABC = 90 degrees, angle AEC can be calculated as follows:
- Angle AEC = Angle ABC - Angle ABE
- Angle AEC = 90 degrees - 60 degrees = 30 degrees.
Final Answer
Thus, angle AEC = 30 degrees.
---
We have a square ABCD and an equilateral triangle ABE constructed outside the square.
1. In a square, all sides are equal and all angles are 90 degrees.
2. In an equilateral triangle, all sides are equal and all angles are 60 degrees.
- Let’s denote the angles of triangle ABE:
- Angle ABE = 60 degrees
- Angle BAE = 60 degrees
- Angle AEB = 60 degrees
- Since ABCD is a square:
- Angle ABC = 90 degrees
- Angle BCD = 90 degrees
- Angle CDA = 90 degrees
- Angle DAB = 90 degrees
- Since ABE is an equilateral triangle, we have:
- AB = BE (sides of the equilateral triangle)
- Since ABCD is a square, we have:
- AB = BC (sides of the square)
Step 6: Conclusion
From the above relationships, we can conclude:
- Since AB = BE and AB = BC, it follows that BC = BE.
- Therefore, triangle ABE is congruent to triangle ABC in terms of side lengths.
To find angle AEC, we can use the property of angles in a triangle:
- Since angle ABE = 60 degrees and angle ABC = 90 degrees, angle AEC can be calculated as follows:
- Angle AEC = Angle ABC - Angle ABE
- Angle AEC = 90 degrees - 60 degrees = 30 degrees.
Thus, angle AEC = 30 degrees.
Topper's Solved these Questions
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-2 )
10 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Multiple Choice Questions) (MATCH THE FOLLOWING)
2 Videos
- TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - NCERT SECTION (Exercise 7.5)
4 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
Knowledge Check
ABCD is square and CDE is an equilateral triangle outside the square. What is the value (in degrees) of ∠BEC?
A15B30C25D10ABCD is square and CDE is an equilateral triangle outside the square. What is the value (in degrees) of ∠BEC ?
A15B30C25D10ABCD is a square and AOB is an equilateral triangle. What is the value of ∠DOC?
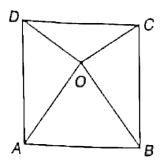 A120∘B150∘C125∘Dcan't be determined
A120∘B150∘C125∘Dcan't be determined
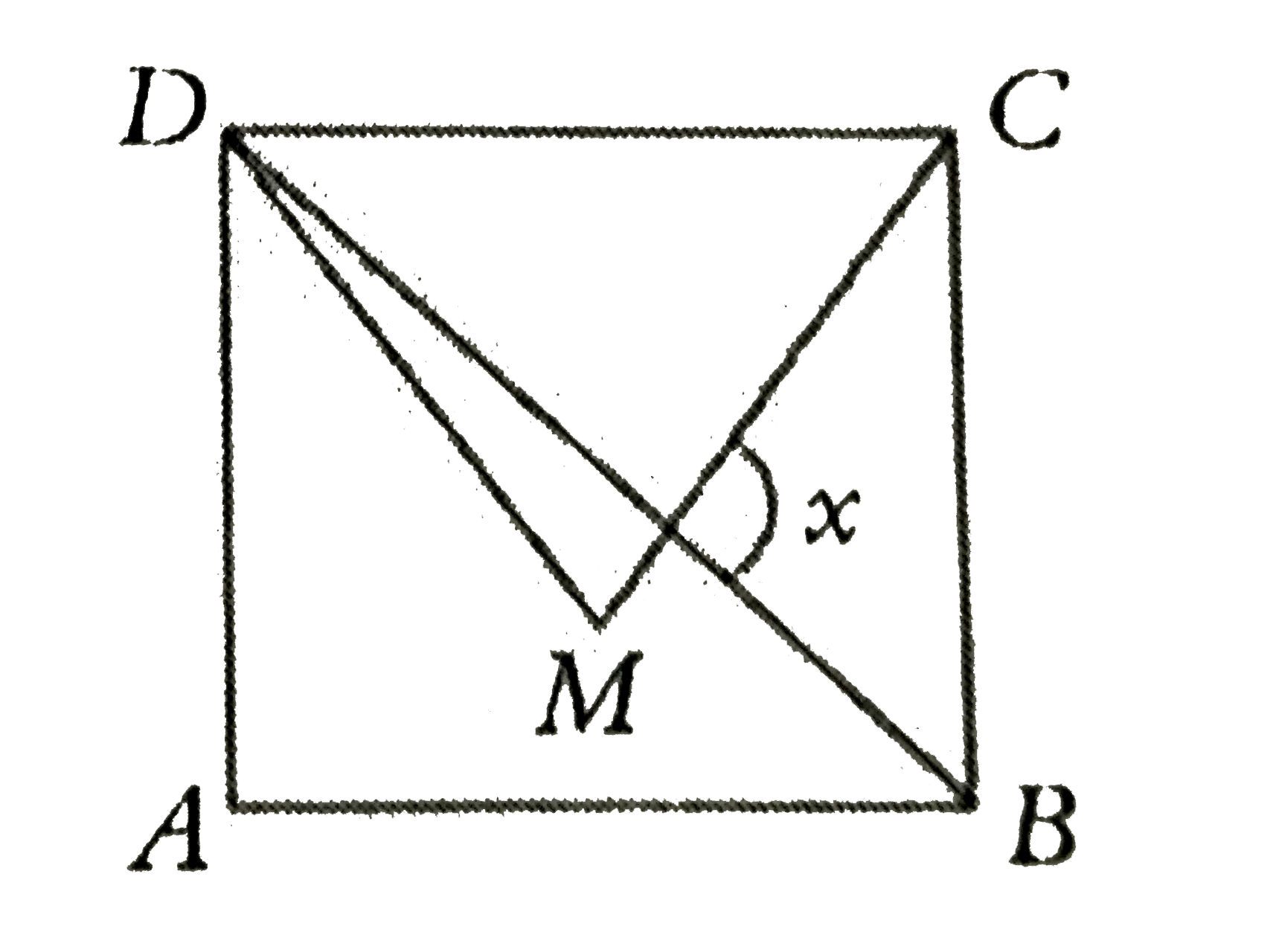
In the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.
View SolutionIn the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find :
(i) ∠APD
(ii) ∠PDC
(iii) ∠DPC
(iv) Prove that DP=CP

View SolutionFind the perimeter of the given figure : BCDE is a square and ABC is an equilateral triangle.

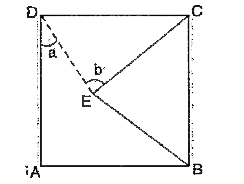
View SolutionABCD is a square and BCE is an equilateral triangle. Find the value of a,b and reflex ∠BED.
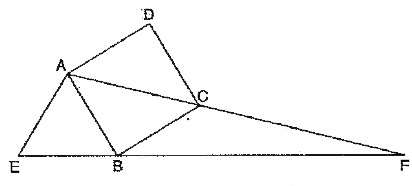
View SolutionABCD is a square, and ABE is an equilateral triangle. ACandEB are produced to meet at F. Calculate the angles of ΔABF.
View Solution
