PQRS is a square. PR and SQ intersect at O. State the measure of ∠POQ.
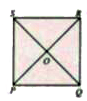
45∘
90∘
180∘
None of these
The correct Answer is:B
Step by step video, text & image solution for PQRS is a square. PR and SQ intersect at O. State the measure of /_POQ. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALS Book:MTG IIT JEE FOUNDATIONChapter:QUADRILATERALS Exercise:EXERCISE (Multiple Choice Questions) (LEVEL-2 )
Explore 15 Videos
- QUADRILATERALS Book:MTG IIT JEE FOUNDATIONChapter:QUADRILATERALS Exercise:EXERCISE (Match the Following)
Explore 2 Videos
- QUADRILATERALS Book:MTG IIT JEE FOUNDATIONChapter:QUADRILATERALS Exercise:NCERT SECTION (Exercise 8.2 )
Explore 11 Videos
- PROBABILITYBook:MTG IIT JEE FOUNDATIONChapter:PROBABILITYExercise:OLYMPIAD/HOTS CORNER
Explore 20 Videos
- STATISTICSBook:MTG IIT JEE FOUNDATIONChapter:STATISTICSExercise:Olympiad/HOTS Corner
Explore 20 Videos
Similar Questions
Knowledge Check
Assertion : ABCD is a square. AC and BD intersect at O. The measure of ∠AOB=90∘
Reason : Diagonals of a square bisect each other at right angles.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.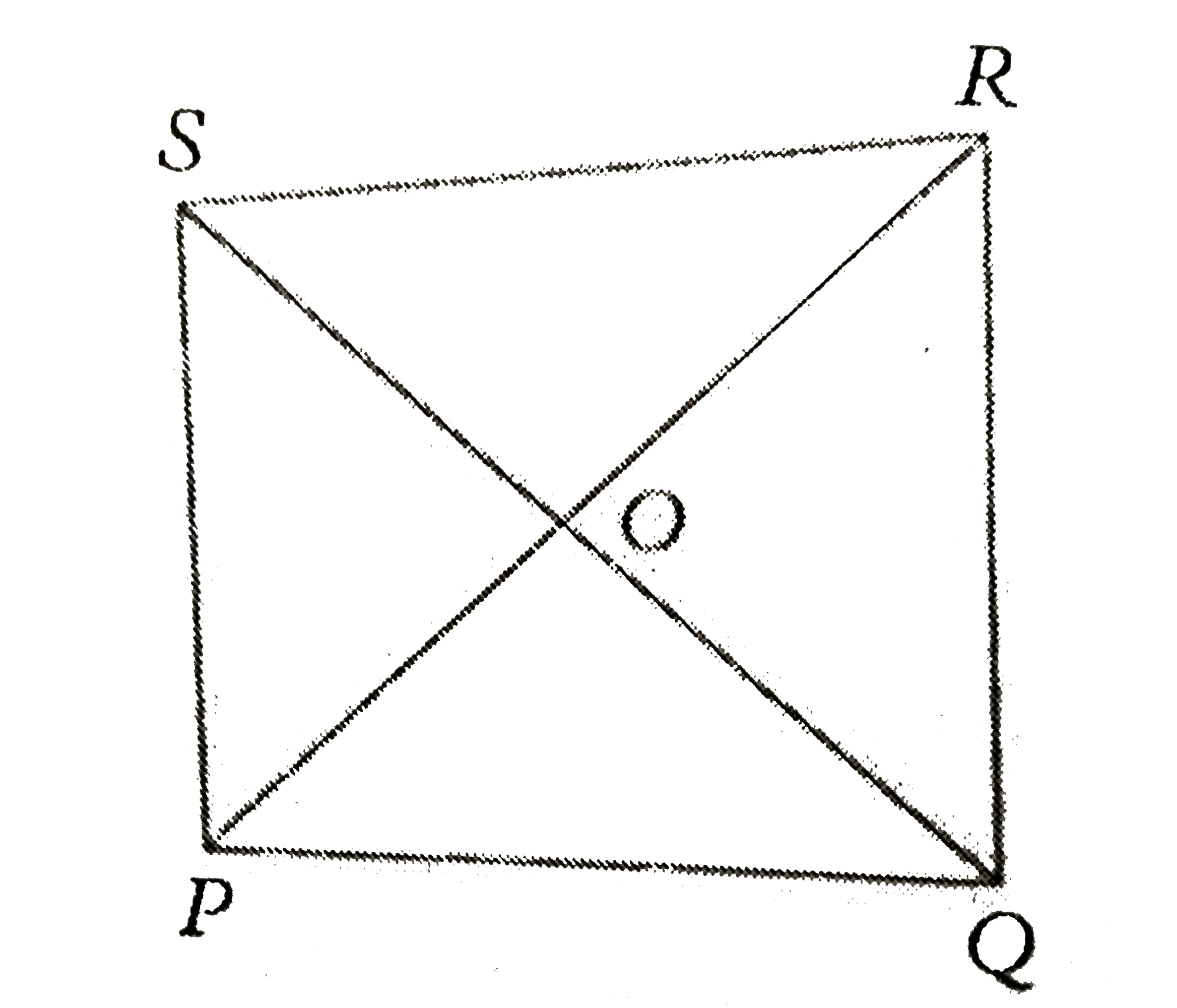
In the given figure, PQRS is a quadrilateral ,PR and QS intersect at O. If ∠PQR=70∘,∠SPQ=80∘,and∠PRQ=60∘, then find ∠SPR.A30∘B50∘C40∘D45∘PQRS is a cyclic quadrilateral. PR and QS intersect at T. If ∠SPR=40∘and∠PQS=80∘, then what is the value (in degrees) of ∠PSR?
A60B40C80D100
PQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
View Solution
In the given figure, PQRS is a quadrilateral ,PR and QS intersect at O. If ∠PQR=70∘,∠SPQ=80∘,and∠PRQ=60∘, then find ∠SPR.
View SolutionPQRS is a cyclic quadrilateral. PR and QS intersect at T. If ∠SPR=40∘and∠PQS=80∘, then what is the value (in degrees) of ∠PSR?
View SolutionPQR is a triangle such that PQ = PR. RS and QT are the median to the sides PQ and PR respectively. If the medians RS and QT intersect at right angle, then what is the value of (PQ/QR)2?
View SolutionPQRS is a square. SR is a tangent (at point S) to the circle with centre O and TR = OS. Then, the ratio of area of the square to the area of the circle is :
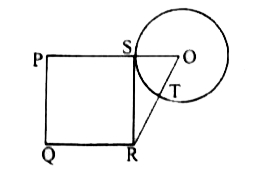
View Solution