PQRS is a cyclic quadrilateral. PR and QS intersect at T. If ∠SPR=40∘and∠PQS=80∘, then what is the value (in degrees) of ∠PSR?
60
40
80
100
To solve the problem, we will use the properties of cyclic quadrilaterals and the angles formed by intersecting chords.
1. Identify the Given Angles:
We have the following angles given in the problem:
- ∠SPR=40∘
- ∠PQS=80∘
2. Use the Property of Cyclic Quadrilaterals:
In a cyclic quadrilateral, the opposite angles are supplementary. This means that:
∠PSR+∠PQR=180∘
3. Find the Angle ∠PQR:
Since ∠PQS and ∠PQR are angles subtended by the same chord PS, we can use the property of angles subtended by the same chord:
∠PQS=∠PSR
Therefore,
∠PQR=80∘
4. Calculate ∠PSR:
Now we can substitute ∠PQR into the supplementary angle equation:
∠PSR+80∘=180∘
Rearranging gives:
∠PSR=180∘−80∘=100∘
5. Final Answer:
Thus, the value of ∠PSR is 100∘.
Summary:
The value of ∠PSR is 100∘.
We have the following angles given in the problem:
- ∠SPR=40∘
- ∠PQS=80∘
In a cyclic quadrilateral, the opposite angles are supplementary. This means that:
∠PSR+∠PQR=180∘
Since ∠PQS and ∠PQR are angles subtended by the same chord PS, we can use the property of angles subtended by the same chord:
∠PQS=∠PSR
Therefore,
∠PQR=80∘
Now we can substitute ∠PQR into the supplementary angle equation:
∠PSR+80∘=180∘
Rearranging gives:
∠PSR=180∘−80∘=100∘
Thus, the value of ∠PSR is 100∘.
The value of ∠PSR is 100∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
PQRS is a cyclic quadrilateral. PR and QS intersect at T. If ∠SPR=40∘and∠PQS=80∘, then what is the value (in degrees) of ∠PSR?
A60B40C80D100ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠CAB=48∘, then what is the value (in degrees) of ∠ADC?
A52B77C138D142PQRS is a cyclic quadrilateral and PQ is the diameter of circle . If ∠RPQ=38∘ , what is the value (in degrees) of ∠PSR ?
A52B77C128D142
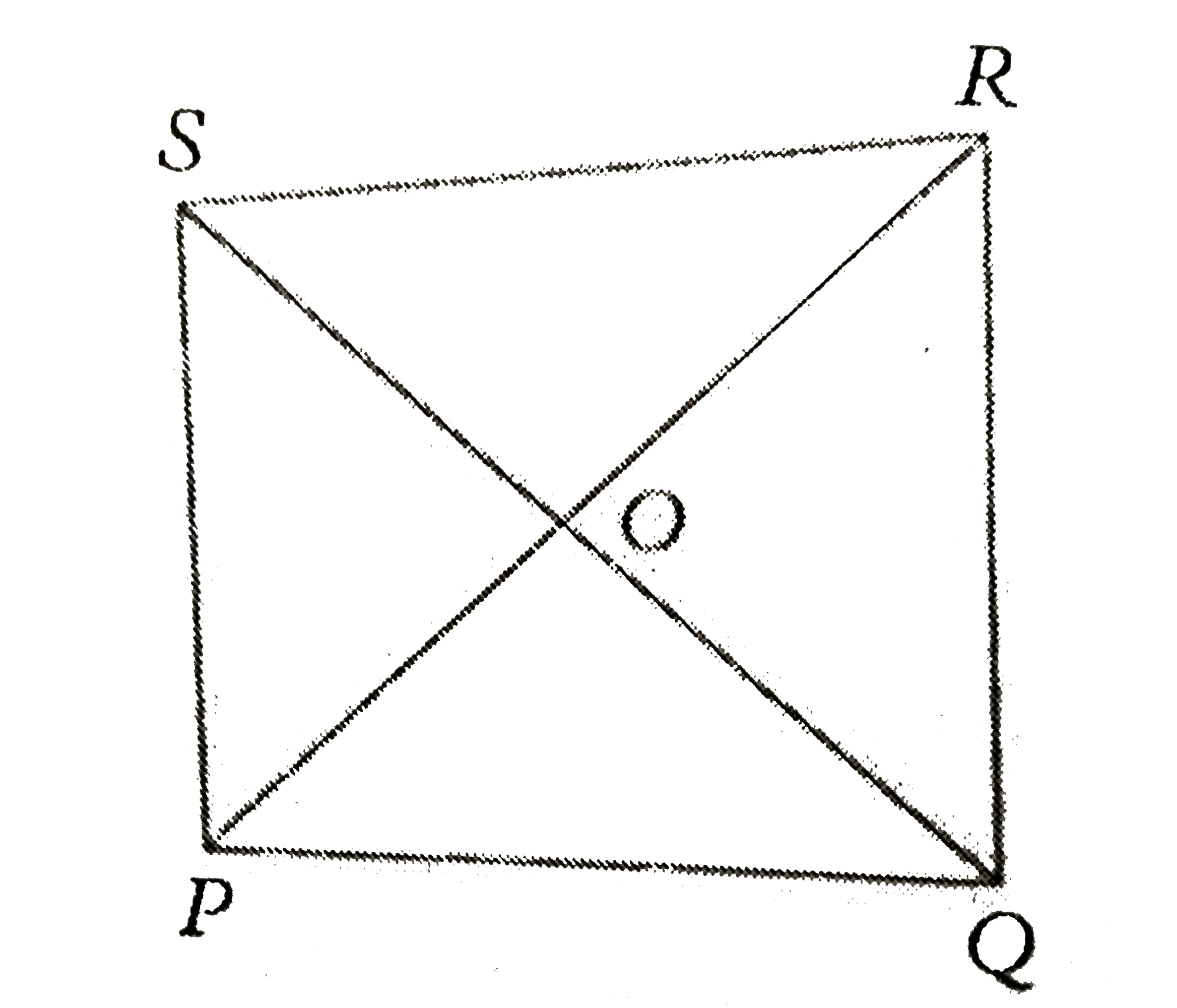
In the given figure, PQRS is a quadrilateral ,PR and QS intersect at O. If ∠PQR=70∘,∠SPQ=80∘,and∠PRQ=60∘, then find ∠SPR.
View SolutionCircum-centre of ΔPQR is O. If ∠QPR=55∘ and ∠QRP=75∘, what is the value (in degrees) of ∠OPR?
View SolutionIn ΔPQR,SandT are the mid points of sides PQ and PR respectively. If ∠QPR=45∘and∠PRQ=55∘, then what is the value (in degrees) of ∠QST ?
View SolutionPQR is a triangle in which PR=QR. Side PR is extended to S, such that QR=RS. If ∠QPR=40∘, then what is the value (in degrees) of ∠QSR?
View SolutionIn triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQR and ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
View Solution
