In the given figure, ABCD is a quadrilateral, the line segments bisecting ∠Cand∠D meet at E. Then 2∠CED is equal to

A
∠A+∠B
B
∠A+∠C
C
∠B+∠D
D
∠C+∠D
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Match the Following)
2 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Assertion & Reason Type)
5 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Multiple Choice Questions) (LEVEL-1 )
35 Videos
- PROBABILITYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
Knowledge Check
In the given figure, the measure of ZC is equal to ∠C
 A90∘B80∘C75∘D95∘
A90∘B80∘C75∘D95∘If ABCD is a cyclic quadrilateral with ∠A=50∘,∠B=80∘ , then ∠C and ∠D are
A130∘,100∘B115∘,115∘C110∘,120∘D130∘,100∘In the following figure, ABCD and AEFG are two parallelograms. If ∠C=55∘ find ∠F.
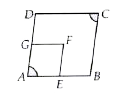 A65∘B75∘C85∘D55∘
A65∘B75∘C85∘D55∘
In the given figure , ABCD and AEFG are two parallelograms . If ∠C=55∘, then find ∠F.

View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
∠C=∠D

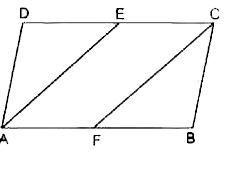
View SolutionIn the adjacent figure , ABCD is a parallelogram and line segments AE and CF bisect the angles A and C respectively . Show that AE∣∣CF.
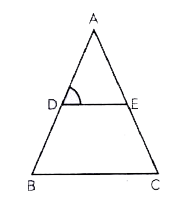
View SolutionIn the given figure, if ∠D=∠C, then it is true that △ADE~△ACB? Why?
View SolutionIf the bisector of the angles A and B of a quadrilateral ABCD meet at O, then ∠AOB is equal to:
View Solution
