Let ABC be an isosceles triangle with AB=AC and let D,E,F be the mid-points of BC,CA and AB respectively. Show that AD⊥FE and AD is bisected by FE.
Step by step video & image solution for Let A B C be an isosceles triangle with A B=A C and let D , E ,F be the mid-points of B C ,C A and A B respectively. Show that A D_|_F E and A D is bisected by F Edot by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Subjective Problems) (Long Answer Type)
5 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Integer/Numerical Value Type)
10 Videos
- QUADRILATERALS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - QUADRILATERALS EXERCISE - EXERCISE (Subjective Problems) (Very Short Answer Type)
10 Videos
- PROBABILITYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- STATISTICSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
Let ABC be an isosceles triangle with AB=AC and let D, E, F be the mid points of BC, CA and AB respectively. Show that AD⊥FE and AD is bisected by FE
View SolutionLet ABC be an isosceles triangle with AB=AC and let D,E,F be the mid-points of BC,CA and AB respectively. Show that AD⊥FE and AD is bisected by FE.
"
View SolutionLet ABC be an isosceles triangle in which AB=AC If D,E,F be the mid-points of the sides BC, CA and AB respectively, show that the segment AD and EF bisect each other at right angles.
View SolutionABC is an isosceles triangle in which AB=AC. If DandE are the mid-points of ABandAC respectively, prove that the points B,C,DandE are concylic.
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
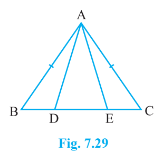
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
View SolutionD, E, F are the mid-points of the sides BC, CA and AB respectively of a ABC . Determine the ratio of the areas of DEF and ABC .
View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View Solution
