The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
Two parts of equal area
Two parts of area in 2 : 1
Two parts of area in 1 : 3
Two parts of area in 4 : 3
The correct Answer is:A
Step by step video solution for The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The diagonals of a parallelogram ABCD intersect at a point O. Through O , a time is drawn to intersect AD at P and BC at Q . Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View Solution
Knowledge Check
AY and BZ are the diagonals of a parallelogram ABYZ, intersecting at O.ar(ΔBYZ) = ?
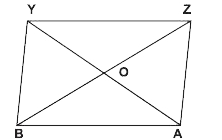 Agreater than ar(ΔABZ)Bis equal to ar(ΔBOA+ΔBOY)Cmore than ar(ΔBOA+ΔBOY)Dless than ar(ΔBOA+ΔBOY)
Agreater than ar(ΔABZ)Bis equal to ar(ΔBOA+ΔBOY)Cmore than ar(ΔBOA+ΔBOY)Dless than ar(ΔBOA+ΔBOY)
The diagonals of a parallelogram ABCD intersect at O.A line through O intersects AB at X and DC at Y. Prove that OX=OY.
View SolutionThe diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
View SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View Solutiondiagonal of a cocyclic parallelogram ABCD is AC and BD intersection at point R. then
View SolutionIn ABC , PQ is a line segment intersecting AB at P and AC at Q such that PQBC and PQ divides ABC into two parts equal in area. Find BPAB .
View SolutionThe diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in x and CD in Y. Show that ar (AXYX)=12(ar||gm ABCD)
View SolutionThe diagonals of a parallelogram ABCD intersect at O. If ∠DBC=30∘ and ∠BDC=60∘, then ∠DAB is
View Solution
