If the medians of ΔPQR intersect at O, then ar (ΔPOQ) =
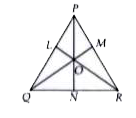
ar (ΔQOR)
13ar(ΔPQR)
Both (a) and (b)
Neither (a) nor (b)
The correct Answer is:C
Step by step video & image solution for If the medians of DeltaPQR intersect at O, then ar (DeltaPOQ) = by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
AY and BZ are the diagonals of a parallelogram ABYZ, intersecting at O.ar(ΔBYZ) = ?
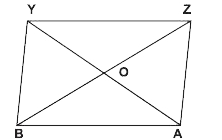 Agreater than ar(ΔABZ)Bis equal to ar(ΔBOA+ΔBOY)Cmore than ar(ΔBOA+ΔBOY)Dless than ar(ΔBOA+ΔBOY)
Agreater than ar(ΔABZ)Bis equal to ar(ΔBOA+ΔBOY)Cmore than ar(ΔBOA+ΔBOY)Dless than ar(ΔBOA+ΔBOY)Assertion (A) : In a trapezium ABCD, we have AB ||DC and the diagonals AC and BD intersect at O.
Then, ar(△AOD)=ar(△BOC).

Reason (R ) : Triangle on the same base between the same parallels are equal in area.ABoth Assertion (A) and Reason (R ) are true and Reason (R ) is a correct explansion of Assertion (A).BBoth Assertion (A) and Reason (R ) are true but Reason (R ) is not a correct explansion of Assertion (A).CAssertion (A) is true and Reason (R ) is false.DAssertion (A) is false and Reason (R ) is true.If PS is median of the triangle PQR, then ar(ΔPQS): ar(ΔQRP) is
 A1 : 1B2 : 1C1 : 2DCan't be determined
A1 : 1B2 : 1C1 : 2DCan't be determined
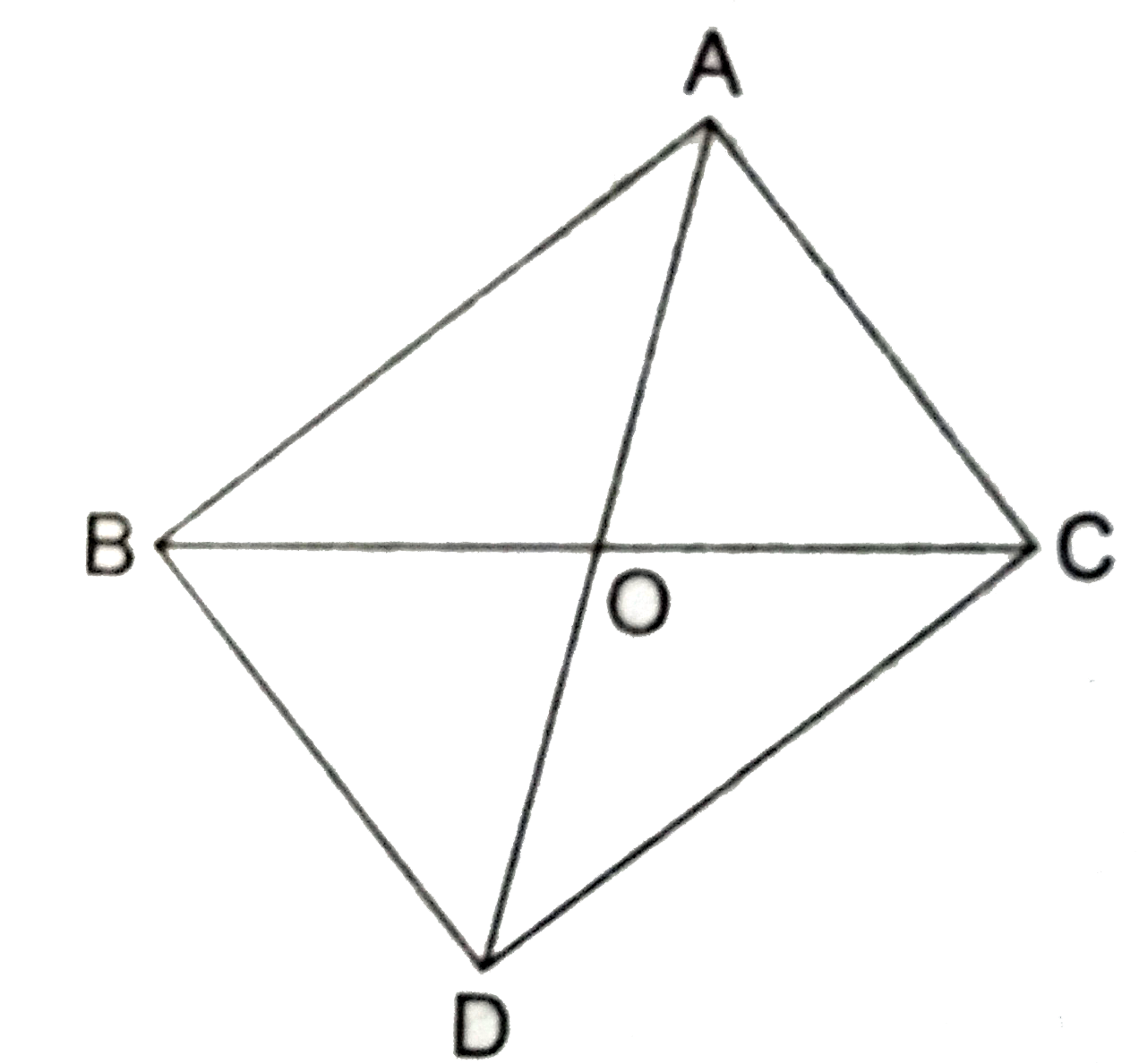
In the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
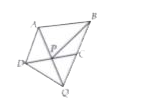
View SolutionIn the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
View SolutionABC is a triangle median CD and BE intersects at point O then find the ratio of area (ΔODE):(ΔABC).
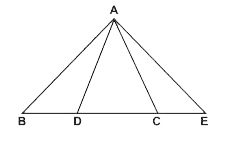
View SolutionIn the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
View Solution