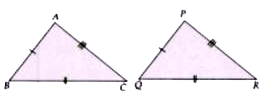
Draw a ΔABC with ∠C=90∘, hypotenuse Ab = 5 cm and side AC = 4 cm. Also, draw a ΔPQR with ∠R=90∘, hypotenus PQ = 5 cm and side PR = 4 cm.
State about the congruency of triangles.
The correct Answer is:ΔABC≅ΔPQR
To solve the problem, we need to draw two right triangles, ΔABC and ΔPQR, and then determine their congruency. Let's go through the steps one by one.
Step 1: Draw Triangle ΔABC
1. Start by drawing a right angle at point C.
2. Label the right angle as ∠C=90∘.
3. From point C, draw line segment AC measuring 4 cm.
4. Now, draw the hypotenuse AB measuring 5 cm. To do this, use a compass or ruler to ensure the length is accurate.
5. Finally, connect points A and B to complete triangle ABC.
Step 2: Draw Triangle ΔPQR
1. Similarly, draw a right angle at point R.
2. Label the right angle as ∠R=90∘.
3. From point R, draw line segment PR measuring 4 cm.
4. Now, draw the hypotenuse PQ measuring 5 cm.
5. Connect points P and Q to complete triangle PQR.
Step 3: Analyze the Congruency of Triangles
1. Both triangles ΔABC and ΔPQR have a right angle (90 degrees).
2. The hypotenuse AB of triangle ABC is equal to the hypotenuse PQ of triangle PQR (both are 5 cm).
3. The side AC of triangle ABC is equal to the side PR of triangle PQR (both are 4 cm).
4. Since both triangles have one right angle, one pair of equal sides (the hypotenuses), and another pair of equal sides, we can conclude that the triangles are congruent by the RHS (Right angle-Hypotenuse-Side) congruence criterion.
Conclusion:
Thus, we can state that ΔABC≅ΔPQR by the RHS congruence criterion.
---
1. Start by drawing a right angle at point C.
2. Label the right angle as ∠C=90∘.
3. From point C, draw line segment AC measuring 4 cm.
4. Now, draw the hypotenuse AB measuring 5 cm. To do this, use a compass or ruler to ensure the length is accurate.
5. Finally, connect points A and B to complete triangle ABC.
1. Similarly, draw a right angle at point R.
2. Label the right angle as ∠R=90∘.
3. From point R, draw line segment PR measuring 4 cm.
4. Now, draw the hypotenuse PQ measuring 5 cm.
5. Connect points P and Q to complete triangle PQR.
1. Both triangles ΔABC and ΔPQR have a right angle (90 degrees).
2. The hypotenuse AB of triangle ABC is equal to the hypotenuse PQ of triangle PQR (both are 5 cm).
3. The side AC of triangle ABC is equal to the side PR of triangle PQR (both are 4 cm).
4. Since both triangles have one right angle, one pair of equal sides (the hypotenuses), and another pair of equal sides, we can conclude that the triangles are congruent by the RHS (Right angle-Hypotenuse-Side) congruence criterion.
Thus, we can state that ΔABC≅ΔPQR by the RHS congruence criterion.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Solved Examples24videos
CONGRUENCE OF TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - NCERT Section (Exercise 7.1)9videos
CONGRUENCE OF TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - COMPARING QUANTITIES EXERCISE - Olympaid/HOTS Corner20videos
COMPARING QUANTITIES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLINGEXERCISE - Olympiad / Hots Corner20videos
DATA HANDLING
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔPQR,∠PQR=90∘,PQ=5cmandQR=12cm. What is the radius (in cm) of the circum-circle of ΔPQR?
A6.5B7.5C13D15 - Question 2 - Select One
In △ABC, ∠B=90∘ , AB=5cm and AC=13cm. Then, BC = ?
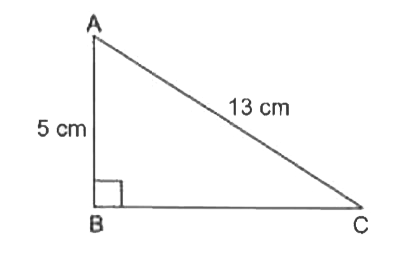 A8 cmB18 cmC12 cmDnone of these
A8 cmB18 cmC12 cmDnone of these - Question 3 - Select One
In ΔABC,AB=4cm,AC=5cmandBC=6cm In ΔPQR,PR=4cm,PQ=5cmandRQ=6cm.ΔABC is congruent to
AΔRPQBΔPQRCΔPRQDΔQRP
In a triangle PQR,∠PQR=90∘,PQ=10cmandPR=26cm, then what is the value (in cm) of inradius of incircle?
View SolutionIn ΔPQR right angled at Q , PQ = 3 cm and PR = 6 cm .
Determine side QR.View SolutionDraw a right triangle whose hypotenuse is of length 4 cm and one side is of length 2.5 cm.
View SolutionIn ΔPQR,∠PQR=90∘,PQ=5cmandQR=12cm. What is the radius (in cm) of the circum-circle of ΔPQR?
View SolutionIn an isosceles triangle ABC,∠B=90∘ and side AB=6cm. Side AC will be
View Solution