In the figure $¯ ¯¯¯¯ ¯ A B ∣ ∣ ¯ ¯¯¯¯ ¯ X Y$ . BX and AY are the transversals intersecting at O, such that $¯ ¯¯¯¯ ¯ O A = ¯ ¯¯¯¯ ¯ O Y$ . Show that $Δ O A B ≅ Δ O Y X$ .

Video Solution

|

Answer

Step by step video & image solution for In the figure bar(AB)||bar(XY). BX and AY are the transversals intersecting at O, such that bar(OA)=bar(OY). Show that DeltaOAB~=DeltaOYX. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.

Updated on:21/07/2023

Class 7 MATHS CONGRUENCE OF TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

In the figure above, $¯ ¯¯¯¯ ¯ A B || ¯ ¯¯¯¯ ¯ C D$ . Find the value of x.
A $50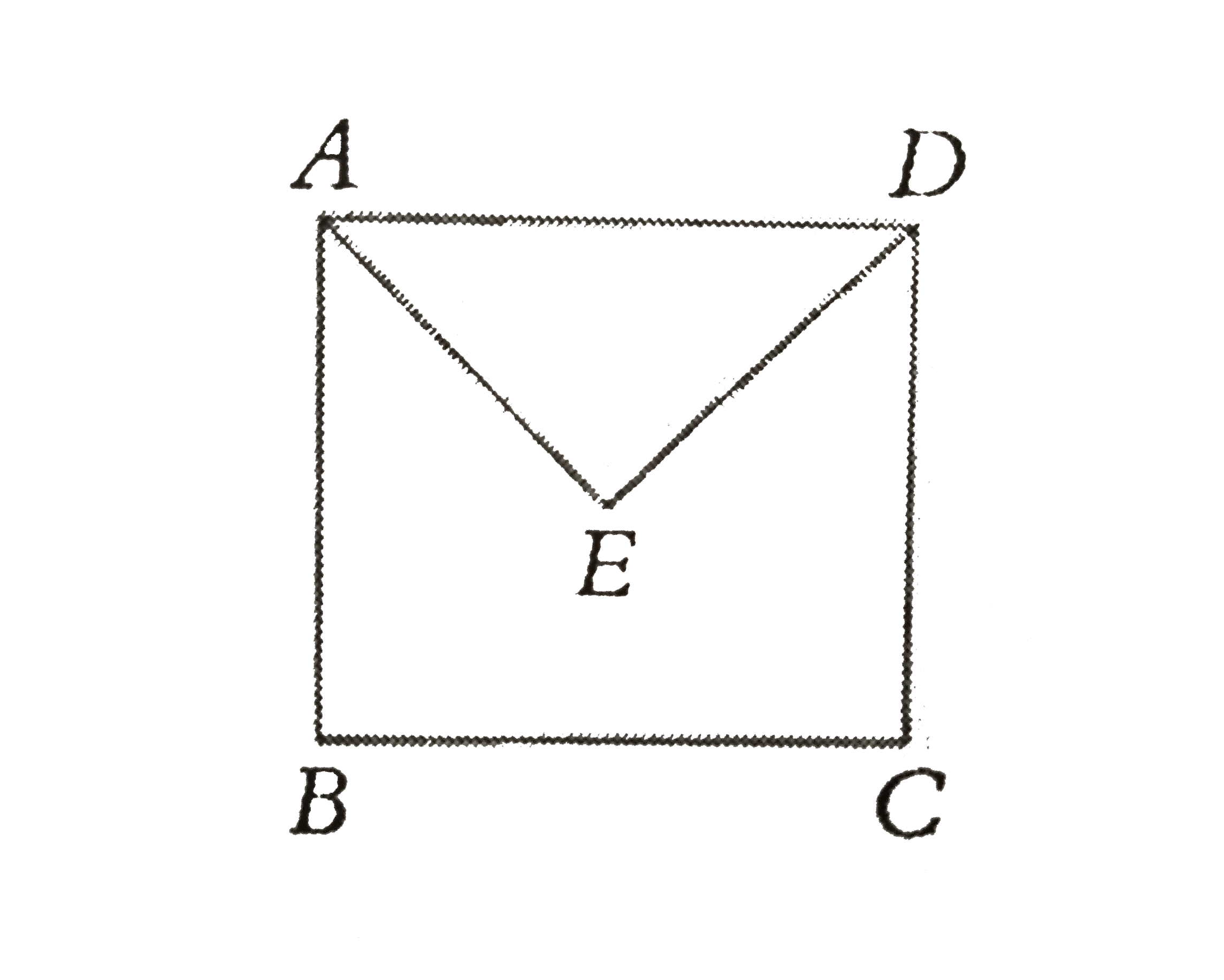^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $40^{\circ}$
Question 2 - Select One

In the figure above, $¯ ¯¯¯¯ ¯ A B ∣ ∣ ¯ ¯¯¯¯ ¯ C D, ∠ B A E = 30^{\circ}$ and $∠ C D E = 35^{\circ}$ . If $¯ ¯¯¯¯ ¯ A B ⊥ ¯ ¯¯¯¯ ¯ B C$ , then find $∠ A E D$ .
A $60^{\circ}$
B $55^{\circ}$
C $65^{\circ}$
D $85^{\circ}$

MTG IIT JEE FOUNDATION-CONGRUENCE OF TRIANGLES -Subjective Problems (Short Answer Type)

Home
Ask Doubt
Profile