In ΔABC,AD⊥BCandAD2=BD⋅CD . Prove that ∠BAC=90∘ .
The correct Answer is:=90∘
To prove that angle ∠BAC=90∘ in triangle ΔABC given that AD⊥BC and AD2=BD⋅CD, we can follow these steps:
Step 1: Understand the Given Information
We are given a triangle ΔABC with a point D on line segment BC such that AD is perpendicular to BC. This means that ∠ADB=90∘.
Step 2: Apply the Pythagorean Theorem
In triangle ADB:
- By the Pythagorean theorem, we have:
AB2=AD2+BD2(1)
In triangle ADC:
- Again, by the Pythagorean theorem, we have:
AC2=AD2+CD2(2)
Step 3: Combine the Equations
Now we can add equations (1) and (2):
AB2+AC2=(AD2+BD2)+(AD2+CD2)
This simplifies to:
AB2+AC2=2AD2+BD2+CD2(3)
Step 4: Substitute the Given Condition
From the problem, we know that:
AD2=BD⋅CD
Substituting this into equation (3):
AB2+AC2=2(BD⋅CD)+BD2+CD2
Step 5: Simplify the Right Side
We can factor the right side:
AB2+AC2=BD2+2BD⋅CD+CD2
This can be rewritten as:
AB2+AC2=(BD+CD)2(4)
Step 6: Conclude the Proof
Now, from equation (4), we have:
AB2+AC2=(BD+CD)2
This is the form of the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Thus, we conclude that:
∠BAC=90∘
Final Conclusion
We have proved that ∠BAC=90∘ as required.
---
We are given a triangle ΔABC with a point D on line segment BC such that AD is perpendicular to BC. This means that ∠ADB=90∘.
In triangle ADB:
- By the Pythagorean theorem, we have:
AB2=AD2+BD2(1)
- Again, by the Pythagorean theorem, we have:
AC2=AD2+CD2(2)
Now we can add equations (1) and (2):
AB2+AC2=(AD2+BD2)+(AD2+CD2)
This simplifies to:
AB2+AC2=2AD2+BD2+CD2(3)
From the problem, we know that:
AD2=BD⋅CD
Substituting this into equation (3):
AB2+AC2=2(BD⋅CD)+BD2+CD2
We can factor the right side:
AB2+AC2=BD2+2BD⋅CD+CD2
This can be rewritten as:
AB2+AC2=(BD+CD)2(4)
Now, from equation (4), we have:
AB2+AC2=(BD+CD)2
This is the form of the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Thus, we conclude that:
∠BAC=90∘
We have proved that ∠BAC=90∘ as required.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Subjective Problems) (Short Answer Type)10videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Subjective Problems) (Long Answer Type)7videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Comprehension Type)9videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER20videos
SURFACE AREAS AND VOLUMES
Similar Questions
In a ABC, AD⊥BC and AD2=BD×CD. Prove that ABC is a right triangle.
View SolutionIn ΔABC , AD ⊥ BC such that AD2=BD×CD . Then ΔABC is a _________ at A .
 View Solution
View SolutionThe circumcentre of the ΔABC is O. Prove that ∠OBC+∠BAC=90∘.
View SolutionIn a quadrilateral ABCD, ∠B=90∘andAD2=AB2+BC2+CD2 prove that ∠ACD=90∘ .
View SolutionIn a ABC, AD⊥BC and AD2=BD×CD. prove that ABC is a right triangle.
View SolutionIn an isosceles ΔABC,AB=ACandBD⊥AC . Prove that (BD2−CD2)=2CD⋅AD.
 View Solution
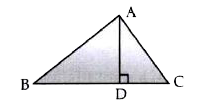
View SolutionIn the figure ∠B=90∘,
AD2=AB2+BC2+CD2.
Prove ∠ACD=90∘ .
 View Solution
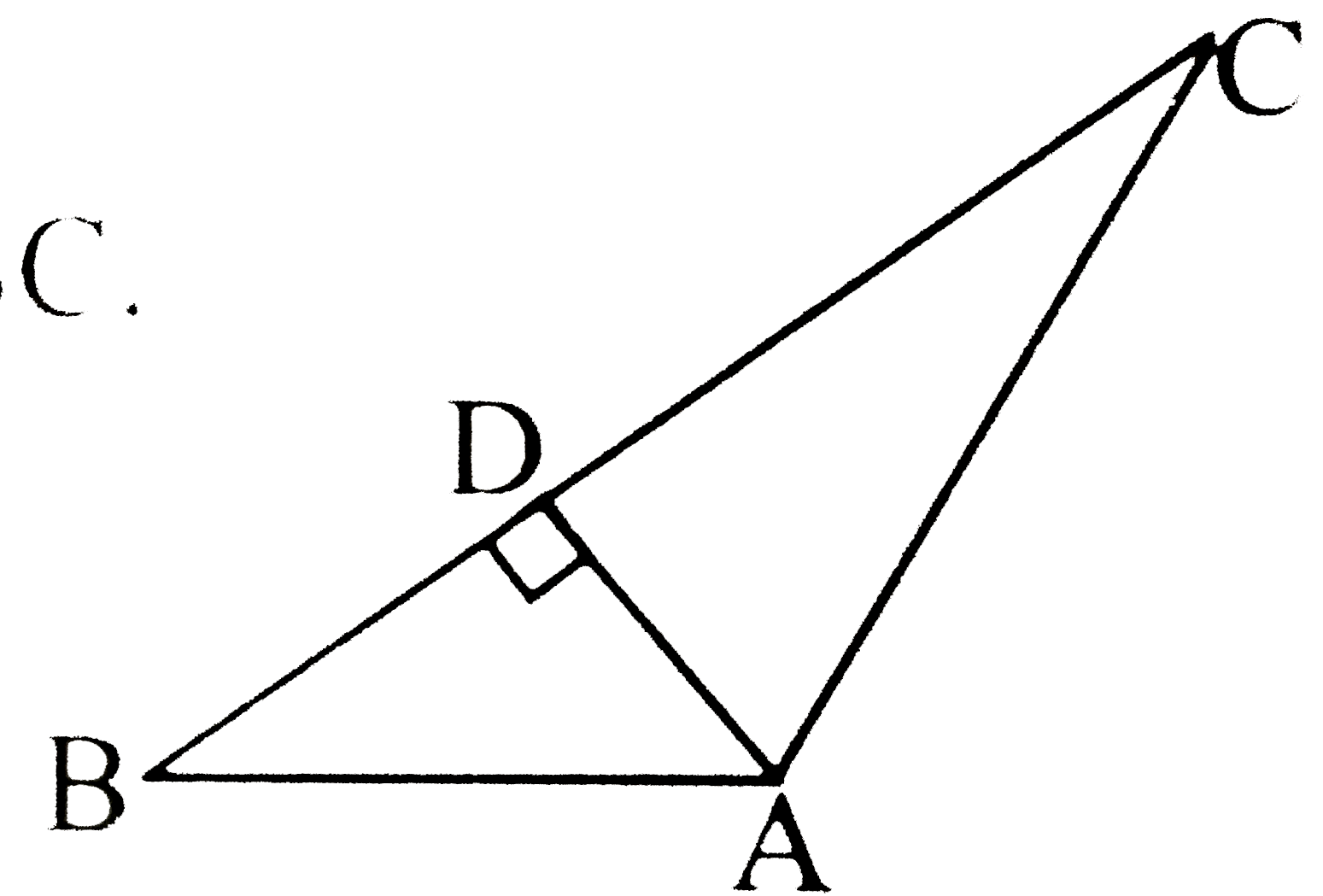
View SolutionSee the given figure. In ΔABC, seg AD⊥ seg BC. Prove that: AB2+CD2=BD2+AC2
 View Solution
View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn ΔABC,AC=BCand∠BAC=50∘. Find ∠BCA.
View Solution

