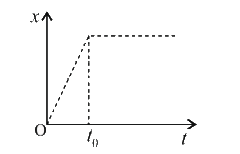
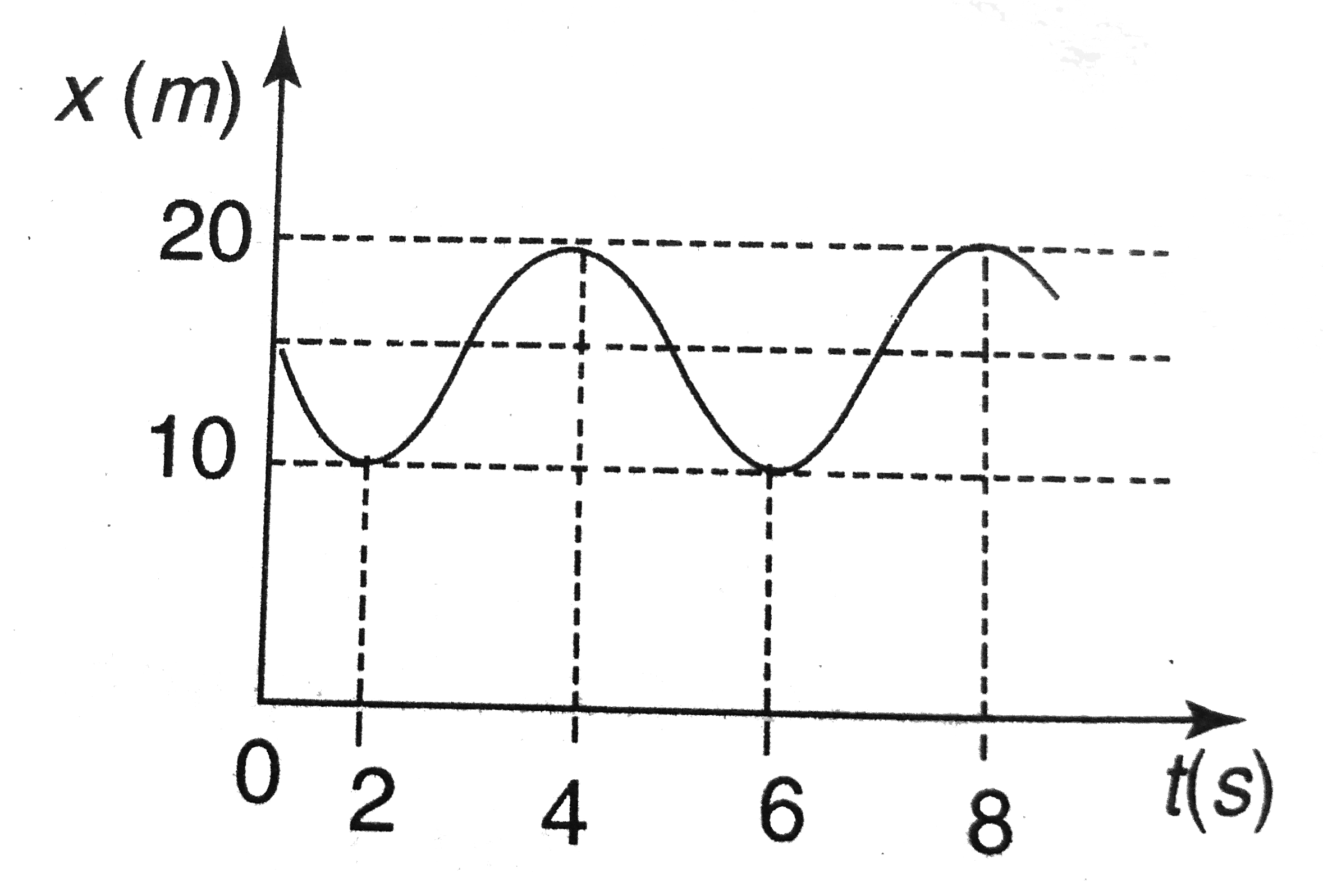
Figure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
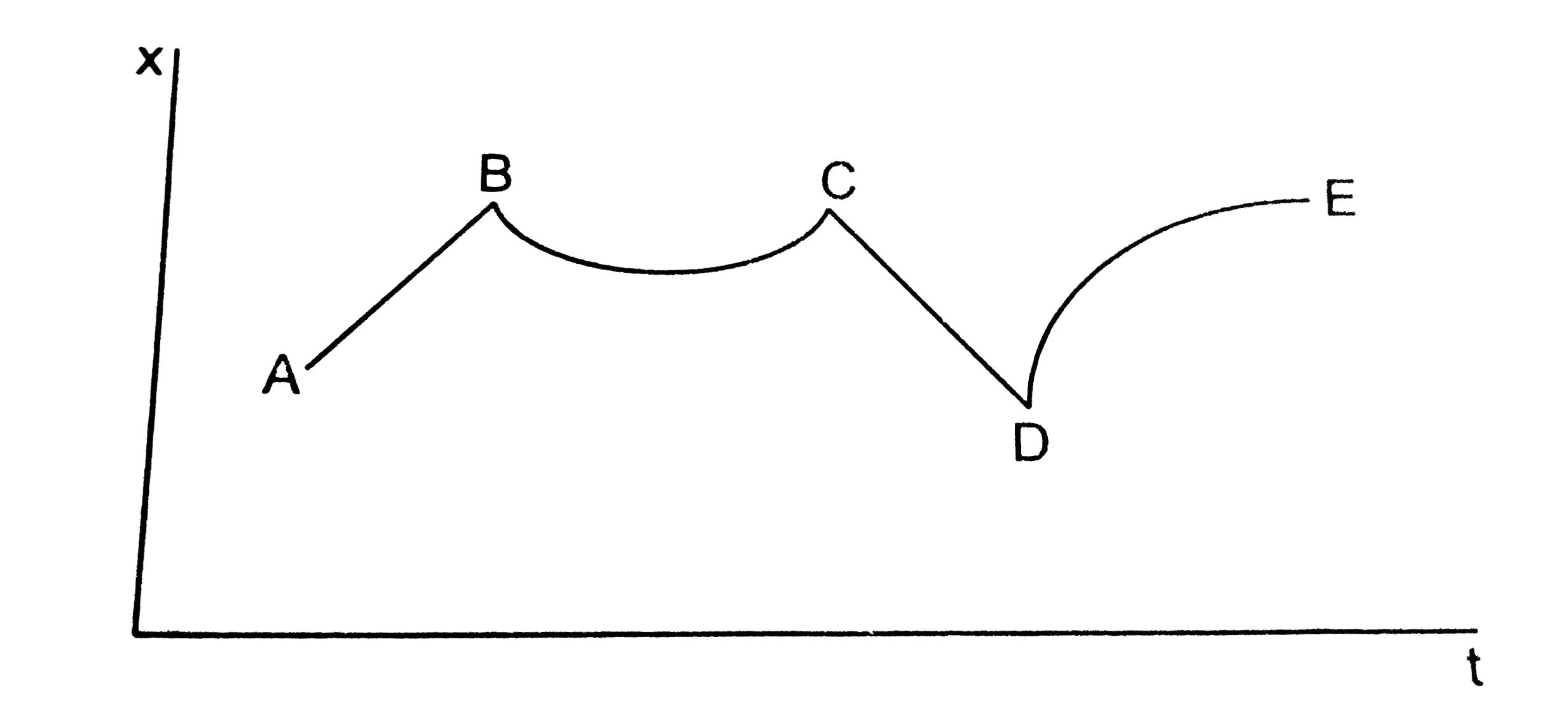
Figure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

A

AB

B

BC

C

CD

D

DE

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

In the region AB, the displacement - time graph is a straight line whereas in all other regions it is curved. Thus, acceleration is zero in the region AB whereas it is non-zero in all other regions
According to Newton.s second law of motion, the force acting on the particle is F = ma
where m is the mass of the particle and a is its acceleration
for region AB = a = 0
∴F=0
Thus, the force acting on the particle is zero is region AB

Updated on:21/07/2023
|
Class 9PHYSICSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

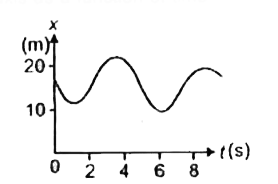
  • Figure shows the position of a particle moving on the X-axis as a function of time.
    ocr_image

    AThe particle has come to rest 6 times
    BThe maximum speed is at t=6 s.
    CThe velocity remains positive for t=0 to t=6s.
    DThe average velocity for the total period shown is negative

  • Figure shows the position of a particle moving on the x - axis as a function of time
    ocr_image

    AThe particle has come to rest 4 times
    BThe velocity at t = 8 s is negative
    CThe velocity remains positive for t = 2 s to t = 6 s
    DThe particle moves with constant velocity.

  • Figure show the displacement - time graph of a particle moving on the x-axis
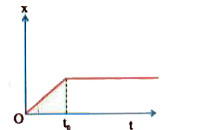    ocr_image

    Athe particle is continuously going in positive X direction
    Bthe particle is at rest
    Cthe velocity increases up to a time t0 and then becomes constant.
    Dthe particle moves at constant velocity up to a time t0 and then stops.