If the length of the wooden cube is 4m and the mass is 1/8 kg, then the relative density of the wooden cube is ______
19.53×10−7
1/512
1/51200
1/32
To find the relative density of the wooden cube, we will follow these steps:
Step 1: Calculate the Volume of the Cube
The volume V of a cube is calculated using the formula:
V=side3
Given that the length of the wooden cube is 4 m, we can calculate the volume as follows:
V=4m×4m×4m=64m3
Step 2: Find the Mass of the Cube
The mass m of the wooden cube is given as:
m=18kg
Step 3: Calculate the Density of the Cube
Density ρ is calculated using the formula:
ρ=massvolume
Substituting the values we have:
ρ=18kg64m3
Calculating this gives:
ρ=18×64=1512kg/m3
Step 4: Convert Density to Standard Form
To express this density in standard form:
ρ=1.953×10−3kg/m3
Step 5: Calculate the Relative Density
Relative density (also known as specific gravity) is calculated using the formula:
Relative Density=Density of the substanceDensity of water
The density of water is approximately 1000kg/m3. Therefore:
Relative Density=1.953×10−3kg/m31000kg/m3
Calculating this gives:
Relative Density=1.953×10−6
To express this in a more readable form:
Relative Density=19.53×10−7
Final Answer
Thus, the relative density of the wooden cube is:
Relative Density=19.53×10−7
---
The volume V of a cube is calculated using the formula:
V=side3
Given that the length of the wooden cube is 4 m, we can calculate the volume as follows:
V=4m×4m×4m=64m3
The mass m of the wooden cube is given as:
m=18kg
Density ρ is calculated using the formula:
ρ=massvolume
Substituting the values we have:
ρ=18kg64m3
Calculating this gives:
ρ=18×64=1512kg/m3
To express this density in standard form:
ρ=1.953×10−3kg/m3
Relative density (also known as specific gravity) is calculated using the formula:
Relative Density=Density of the substanceDensity of water
The density of water is approximately 1000kg/m3. Therefore:
Relative Density=1.953×10−3kg/m31000kg/m3
Calculating this gives:
Relative Density=1.953×10−6
To express this in a more readable form:
Relative Density=19.53×10−7
Thus, the relative density of the wooden cube is:
Relative Density=19.53×10−7
Similar Questions
In Fig. a cube of edge length L=0.500 m and mass 450 kg is suspended by a rope in an open tank of liquid of density 1030 kg/m3. Find (a) the magnitude of the total downward force on the top of the cube from the liquid and the atmosphere, assuming atmospheric pressure is 1.00 atm, (b) the magnitude of the total upward force on the bottom of the cube, and (c) the tension in the rope. (d) Calculate the magnitude of the buoyant force on the cube using Archimedes' principle. What relation exists among all these quantities?
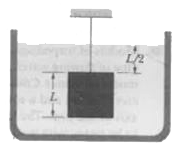 View Solution
View SolutionA wooden block is tied to a metallic rod of mass 100 g and immersed completely in water. When the displaced water is collected in a measuring jar, the volume of the liquid displaced is found to be 400 ml. If the density of the metallic rod is 5 g cm,−3 and the mass of the wooden block is 300 g, determine the density of the wooden block.
View Solution
Knowledge Check
- Question 1 - Select One
A woman of mass 50 kg stands on a wooden block placed over a tank of water. The wooden block is such that the woman is entirely above water. If relative density of wood is 0.85, the volume of the wooden block is:
A0.5×10−1m3B0.585×10−1m3C0.33m3D0.54×10−1m3 - Question 2 - Select One
If the ratio of density of ice to that of wood is (9/8) and the relative density of ice is 0.9, then the density of wood is __________ kg m^(−3)(Takedensityofwater=10^(3) m^(-3)
A0.8B800C8×103DMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMM - Question 3 - Select One
We have a vessel in shape of a cuboid partially filled with water. It base is square wilth an area of 4.5dm2(1dm=10cm) and a vessel contains water up to 2cm height. Then we place wooden cube inside water. The wood has mass 4kg and specific gavity 0.5. The base of the wooden cube is horizontal. Find the height of water level above the base of the wooden block.
A10cmB2cmC15cmD7cm
A wooden block of mass 8kg is tied to a string attached to the bottom of a tank. The block is completely inside the water. Relative density of wood is 0.8. Taking g=10m/s2, What is the tension in the string ?
View SolutionA cone is hollowed out of a solid wooden cube of side 6 cm. The diameter and height of the cone is same as the side of the cube. What is the volume of the remaining cube ?
View SolutionOne boy is carrying a bucket of water by his one hand and wooden cube in his other hand. If he places the wooden cube in the bucket of water, then he will feel
View SolutionA wooden block of mass 8 kg is tied to a string attached to the bottome of the tank. In the equilibrium the block is completely immersed in water. If relative density of wood is 0.8 and g=10ms−2, the tension T, in the string is
View SolutionA metal cube of edge 310 m is melted and formed into three smaller cubes. If the edges of the two smaller cubes are 15 m and 14 m, find the edge of the third smaller cube.
View Solution

