A wooden cube of length l and density a floats in a liquid of density p(>a). If the liquid moves with an acceleration in steady state, find the a. net hydrostatic force acting on the cube b. angle of inclination of the cub with horizontal.

The correct Answer is:ag
F=N=mgcosθ

where cosθ=g√g2+a2 or T=mg2√(g2+a2)
b. tanθ=ag or θ=tan−1ag
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Single Correct
95 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
A container having a liquid of density ρ is moving downwards with acceleration g2. Find the pressure difference between two vertical points in the liquid separated by h
View SolutionA container contains an incompressible and non - viscous liquid of density ρ and is filled upto a height H . Now if container is moved towards right with an acceleration a then find the horizontal force exerted by liquid on the face ABCD of container . Assume container have enough height so that liquid does not fall outside the container .

View Solution
Knowledge Check
A needle of length l and density ρ will float on a liquid of surface tension σ if its radius r is less than or equal to:
A√2σπρlgB√2σlπρgC√σπρgD√2σπρg
A vertical communicating tube contains a liquid of density ρ. If it moves with a horizontal acceleration a, pressure at A is equal to :Aρgh2+P0+2Tr2+ρalBρgh2+ρal+P0−2Tr2Cρgh1+P0−2Tr1Dρgh1−P0−2Tr1
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isAhρgBlρaChρg−lρaDhρg+lρa
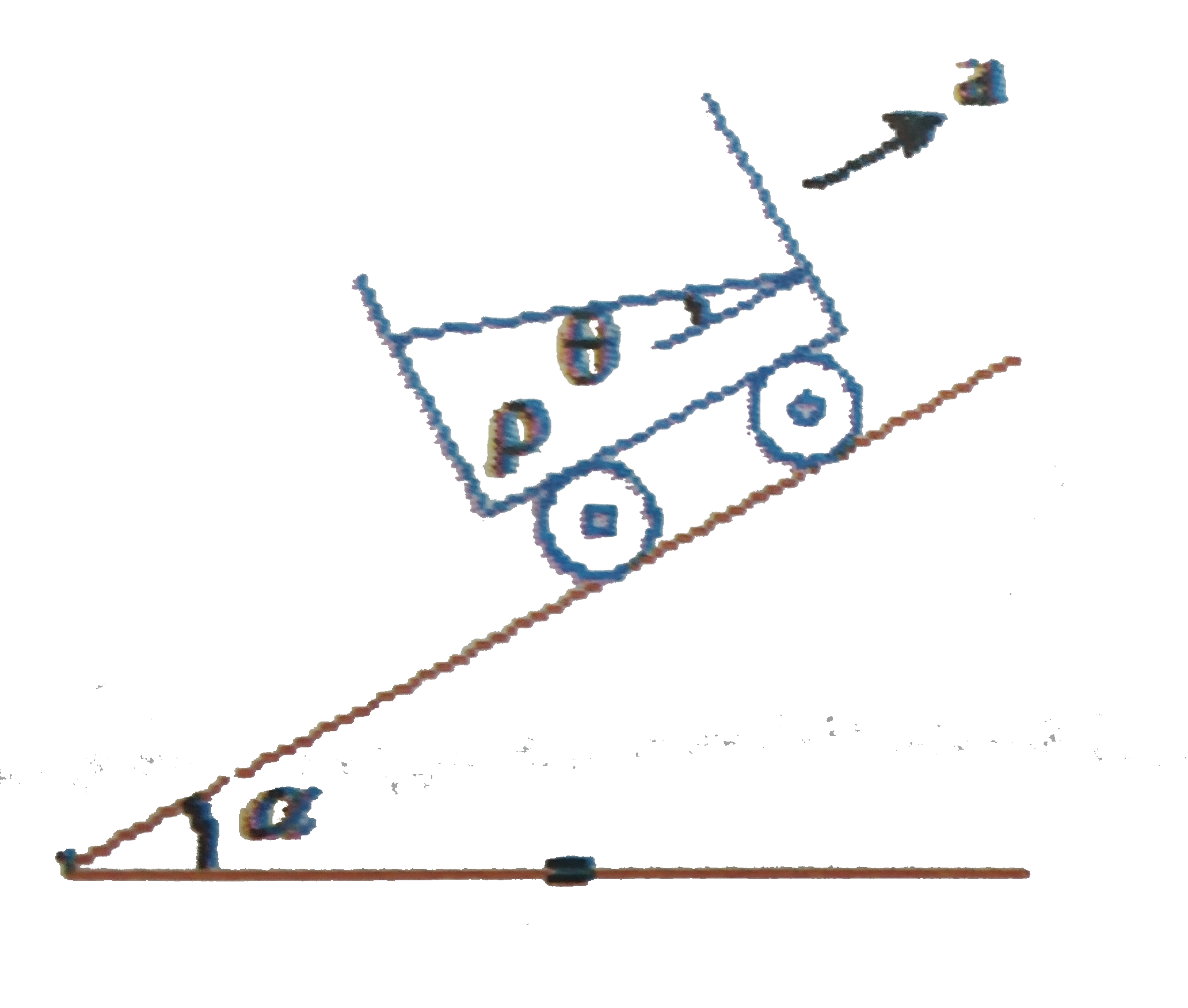
A fluid container is containing a liquid of density ρ is accelerating upward with acceleration a along the inclined plane of inclination α as shown in the figure. Then the angle of inclination θ of free surface is
View SolutionA solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View SolutionA trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.

View SolutionA liquid of density ρ0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density ρ is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination θ of the rod with the horizontal in equilibrium position is
View SolutionA sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be

View Solution