A stone dropped from a building takes 4 s to reach the ground. The height of the building is
The correct Answer is:C
To find the height of the building from which a stone is dropped, we can use the equations of motion under uniform acceleration due to gravity. Here’s a step-by-step solution:
Step 1: Identify the known values
- Time taken (t) = 4 seconds
- Initial velocity (u) = 0 m/s (since the stone is dropped)
- Acceleration due to gravity (g) = 9.8 m/s² (approximately)
Step 2: Use the equation of motion
We will use the second equation of motion:
s=ut+12at2
where:
- s is the distance (height of the building, H)
- u is the initial velocity
- a is the acceleration (which is g in this case)
- t is the time taken
Step 3: Substitute the known values into the equation
Since the initial velocity u=0, the equation simplifies to:
H=0⋅t+12gt2
Substituting the values:
H=12⋅9.8⋅(4)2
Step 4: Calculate H
Calculating (4)2:
(4)2=16
Now substituting back:
H=12⋅9.8⋅16
Calculating 12⋅9.8=4.9:
H=4.9⋅16
Now calculating 4.9⋅16:
H=78.4 meters
Final Answer
The height of the building is 78.4 meters.
---
- Time taken (t) = 4 seconds
- Initial velocity (u) = 0 m/s (since the stone is dropped)
- Acceleration due to gravity (g) = 9.8 m/s² (approximately)
We will use the second equation of motion:
s=ut+12at2
where:
- s is the distance (height of the building, H)
- u is the initial velocity
- a is the acceleration (which is g in this case)
- t is the time taken
Since the initial velocity u=0, the equation simplifies to:
H=0⋅t+12gt2
Substituting the values:
H=12⋅9.8⋅(4)2
Calculating (4)2:
(4)2=16
Now substituting back:
H=12⋅9.8⋅16
Calculating 12⋅9.8=4.9:
H=4.9⋅16
Now calculating 4.9⋅16:
H=78.4 meters
The height of the building is 78.4 meters.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Multiple choice questions12videos
GRAVITATION
- BOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Mock Test (3)25videos
GRAVITATION
- BOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Worksheet4videos
GRAVITATION
- BOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - MOCK TEST36videos
FORCES AND LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - MOTIONEXERCISE - Mock test24videos
MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A stone is dropped from roof of building takes 5 s to reach the ground. The sound of striking is heard after 5.4 second after the stone is dropped. The velocity of sound is
A312.5ms−1B332.5ms−1C352ms−1D392ms−1 - Question 2 - Select One
A stone dropped from a building takes 4 s to reach the ground. The height of the building is
A78.4 mB64 mC260 mD2000 m - Question 3 - Select One
A stone dropped from the top of a tower reaches the ground in 3 s. The height of the tower is
A18.6 mB39.2 mC44.1 mD98 m
A stone falls from a building and reaches the ground 2.5 seconds later. How high is the building? (=9.8m/s2)
View SolutionA body dropped from a height of 5m. Reaches the ground in 1 s. if it takes 2 s to reach the ground , find the height from which it is dropped.
View SolutionA stone is thrown downwards with velocity 10 m/s from the roof of a builng and it reaches the ground with speed 40 m/s. the height of the building would be
View Solutionballoon is rising vertically up with a velocity of 29 m/s. A stone is dropped from it and it reaches the ground in 10 seconds. The height of the balloon when the stone was dropped from it is (g=9.8ms2)
View SolutionThe velocity time graph for the veticaly component of the velocity of a body thrown upwards from the ground and landing on the roof of a building is given in the figure.The height of the building is:
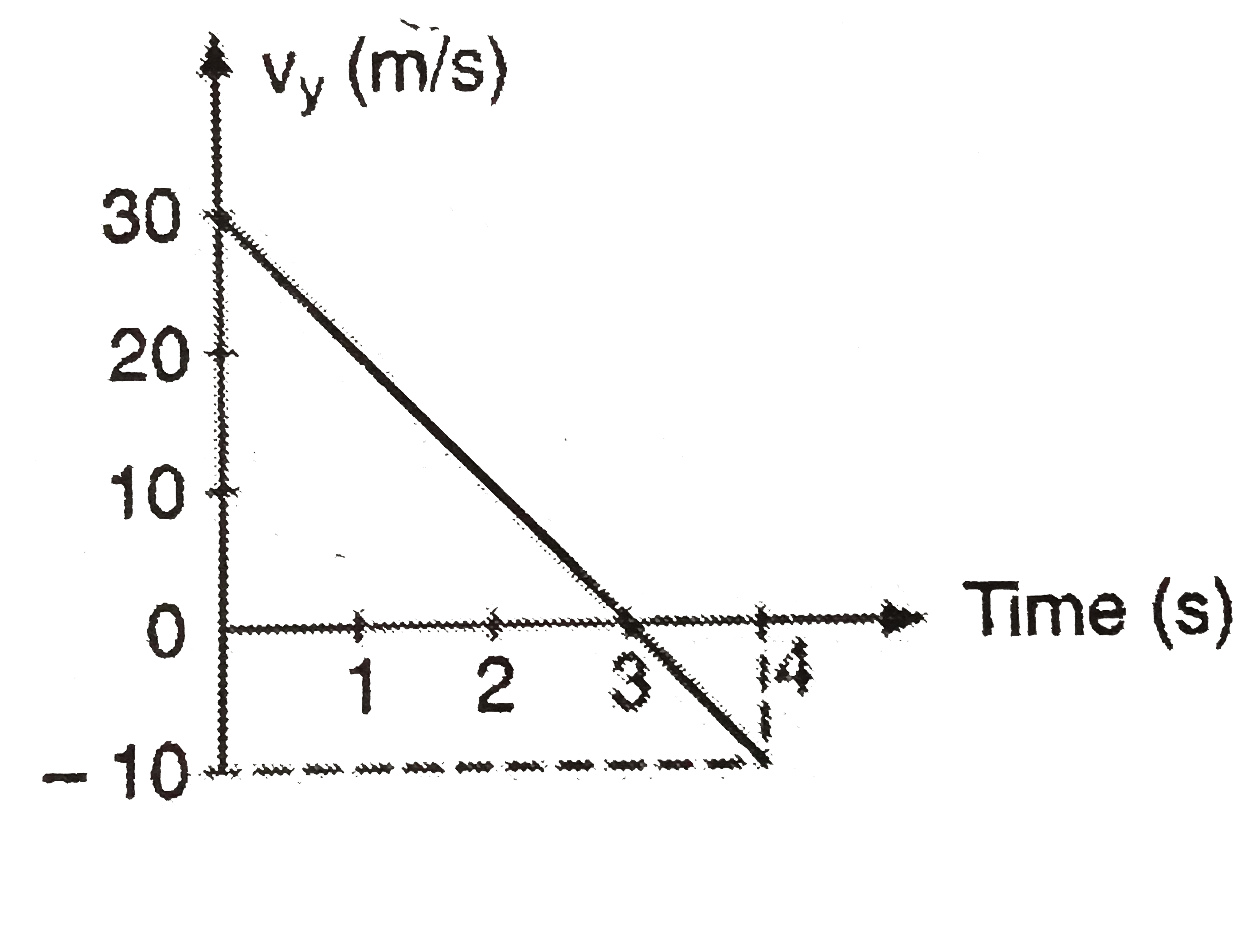 View Solution
View Solution

