Two bodies A and B of mass 500 g and 200 g respectively are dropped near the earth's surface. Let the acceleration of A and B be aA and aB respectively then
aa=aB
aA>aB
aA<aB
aA≠aB
To solve the problem, we need to analyze the situation of two bodies dropped near the Earth's surface. We will determine the relationship between their accelerations, aA and aB.
1. Understanding the Situation:
- We have two bodies:
- Body A with mass mA=500g=0.5kg
- Body B with mass mB=200g=0.2kg
- Both bodies are dropped from rest near the Earth's surface.
2. Identifying the Forces Acting on the Bodies:
- When an object is dropped, the only force acting on it (ignoring air resistance) is the gravitational force.
- The gravitational force F on an object is given by the formula:
F=m⋅g
where g is the acceleration due to gravity (approximately 9.8m/s2 near the Earth's surface).
3. Calculating the Acceleration of Each Body:
- For body A:
FA=mA⋅g=0.5kg⋅9.8m/s2=4.9N
The acceleration aA can be calculated using Newton's second law F=m⋅a:
aA=FAmA=4.9N0.5kg=9.8m/s2
- For body B:
FB=mB⋅g=0.2kg⋅9.8m/s2=1.96N
The acceleration aB can also be calculated using Newton's second law:
aB=FBmB=1.96N0.2kg=9.8m/s2
4. Comparing the Accelerations:
- From the calculations, we find:
aA=9.8m/s2andaB=9.8m/s2
- Therefore, we conclude that:
aA=aB
5. Final Conclusion:
- The accelerations of both bodies A and B are equal, regardless of their masses. Thus, we can state:
aA=aB
- We have two bodies:
- Body A with mass mA=500g=0.5kg
- Body B with mass mB=200g=0.2kg
- Both bodies are dropped from rest near the Earth's surface.
- When an object is dropped, the only force acting on it (ignoring air resistance) is the gravitational force.
- The gravitational force F on an object is given by the formula:
F=m⋅g
where g is the acceleration due to gravity (approximately 9.8m/s2 near the Earth's surface).
- For body A:
FA=mA⋅g=0.5kg⋅9.8m/s2=4.9N
The acceleration aA can be calculated using Newton's second law F=m⋅a:
aA=FAmA=4.9N0.5kg=9.8m/s2
FB=mB⋅g=0.2kg⋅9.8m/s2=1.96N
The acceleration aB can also be calculated using Newton's second law:
aB=FBmB=1.96N0.2kg=9.8m/s2
- From the calculations, we find:
aA=9.8m/s2andaB=9.8m/s2
- Therefore, we conclude that:
aA=aB
- The accelerations of both bodies A and B are equal, regardless of their masses. Thus, we can state:
aA=aB
Similar Questions
Knowledge Check
Let A and B be the points respectively above and below the earth's surface each at a distance equal to half the radius of the earth. If the acceleration due to gravity at these points be gAandgB respectivel, them gB:gA
A1:1B9:8C8:9DzeroFigure shows two blocks each of mass m system is released from rest. If acceleration of blocks A and B at any instant (not initially) are a1 and a2, respectively. Then
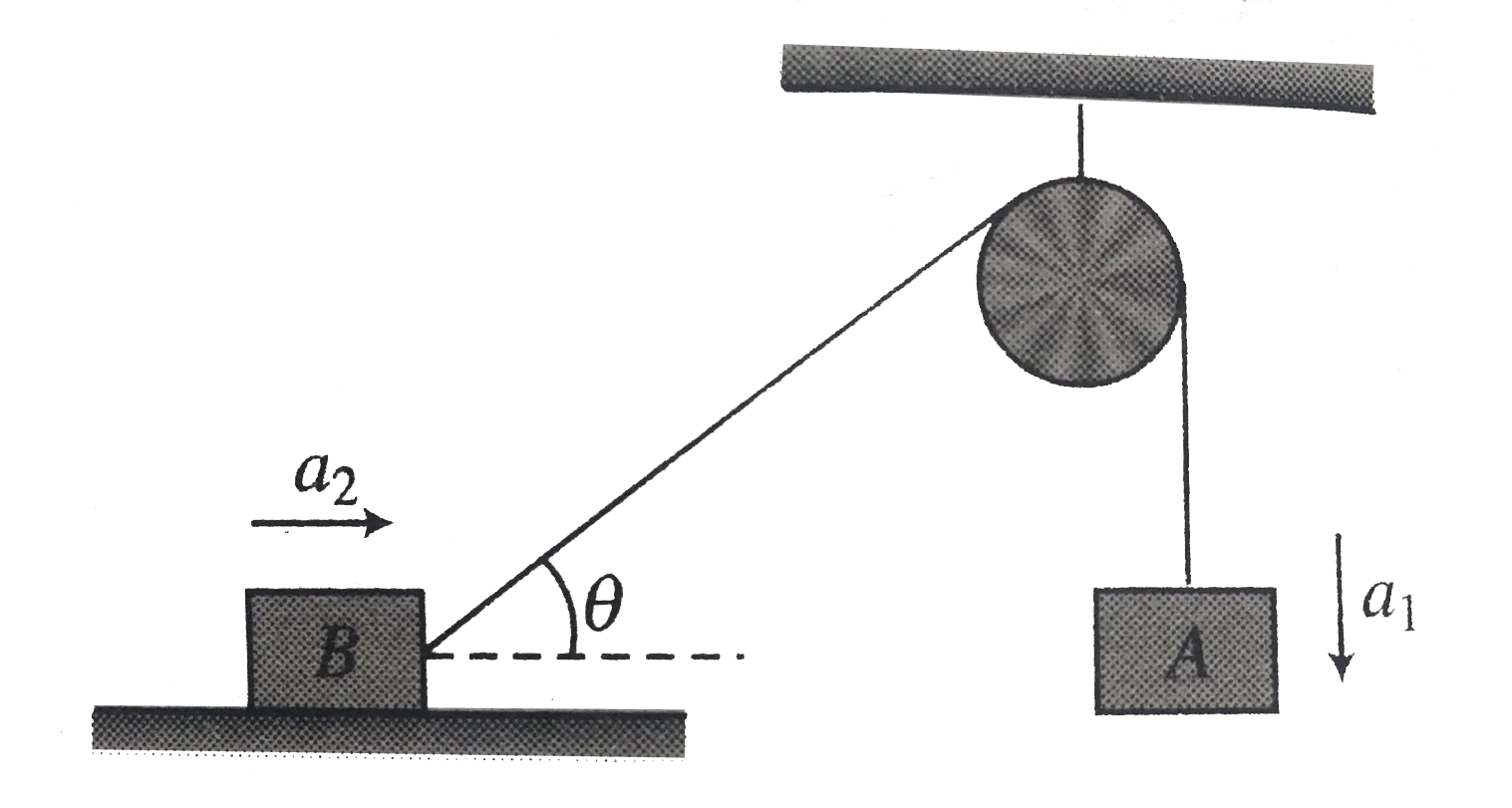 Aa1=a2cos=θBa2=a1cos=θCa1=a2DNone of these
Aa1=a2cos=θBa2=a1cos=θCa1=a2DNone of theseThree blocks A, B, and C of masses 3M,2M, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is a1,a2 and a3 , respectively, then

The value of acceleration a2 at the moment spring TU is cut isAg/5, upwardBg/5 downwardCg/3, upwardDZero
There exists a uniform electric field between plates A and B. An electron and proton, initially at rest are released from plates A and B respectively. If ae and ap stand for the acceleration of electron and proton respectively then
View SolutionThree blocks A, B, and C of masses 3M,2M, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is a1,a2 and a3 , respectively, then

The value of acceleration a1 at the moment string RS is cut is
View SolutionThree blocks A, B, and C of masses 3M,2M, and M are suspended vertically with the help of spring PQ and TU, and a string RS as shown in fig. If the acceleration of blocks A, B and C is a1,a2 and a3 , respectively, then

The value of acceleration a3 at the moment spring PQ is cut is
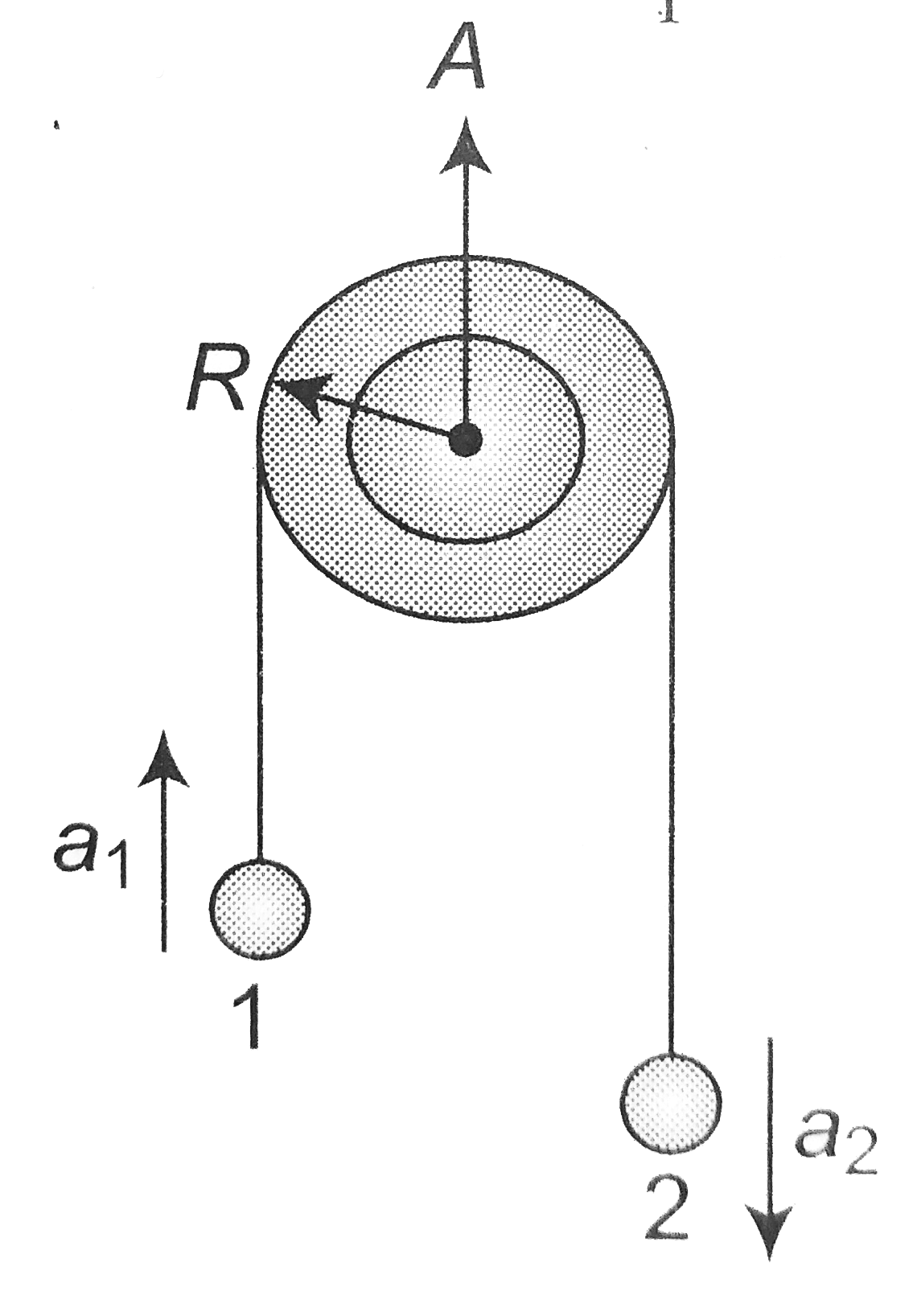
View SolutionTwo masses are connected by a string which passes over a pulley acceleration upward at a rate A shown. If a1 and a2 be the accelerations of bodies 1 and 2 respectively then,
View SolutionIn the figure the block A,B and C of mass m each, have acceleration a1,a2&a3 respectively. F1&F2 are external forces of magnitude 2 mg and mg respectively :
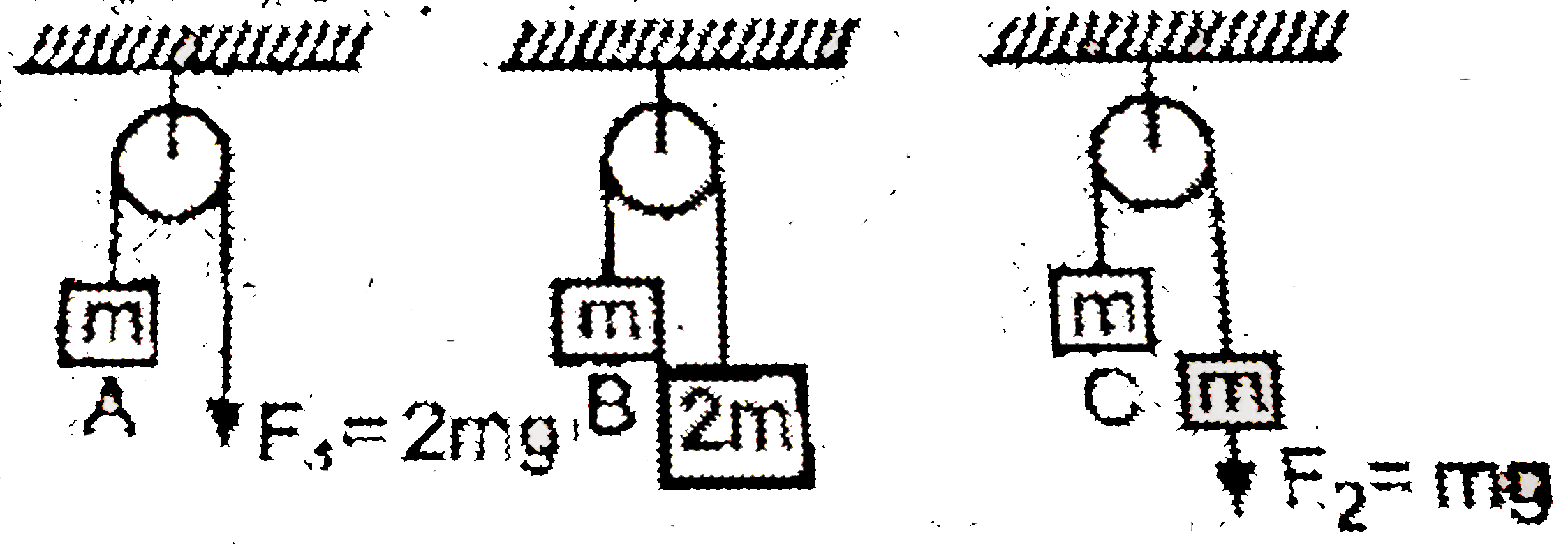
View Solution

