Two capacitor of Unknown capacities can produce maximum capacity 16 farad and minimum 3 farad when connected together. Find the capacity of each capacitor.
Let we have two capacitors C1andC2 These produce maximum capacitance, when connected in parallel
⇒ Cp=16F
⇒ C1+C2=16 ...(i)
These produce minimum capacitance when connected in series
1CS=3F
1CS=1C1+1C2
13=C1+C2C1C2
13=16C1C2
1×C1C2=16×3
1×C1C2=16×3
C1C2=48
Weknow(C1−C2)2=1(C1+C2)2−4C1C2
(C1−C2)2=(16)2−4(48)
=256−192
=64
(C1−C2)2=64
(C1−C2)=√64=8 ...(2)
Adding equation (1) and (2)
C_(1)+cancel(C)_(2)+C_(1)-cancel(C)_(2)=16+8
2C1=24
2C1=24
C1=12F
Put Value of C1 in eq.(2)
12−C2=8
C2=8
C_(2)=12-8<br>C_(2)=4F
Similar Questions
An isolated capacitor of unknown capacitance has been charged to potential V0. This capacitor is then connected to an uncharged capacitor of capacity C. If common potential is V(<V0, find unknow capacitance.
View SolutionThree capacitors each of capacitor 2μF are connected in series. Find resultance capacity in farad.
View Solution
Knowledge Check
Two capacitors of equal capacities when connected in series have some resultant capacity. Then they are connected in parallel. The resultant capacity of parallel combination is
Asame as the series capacityBtwo times of the series capacityCthree times of the series capacityDfour times of the series capacityn capacitors each of capacity C are joined in parallel. If they are connected to a source of V volts, then the energy stored in the capacitor is
ACV2B12nCV2C12nCV2D12nCV2The difference in the effective capacities of two similar capacitors when joined in series and then in parallel is 6μF. The capacity of each capacitor is
A2μFB4μFC8μFD16μF
Figure shows two capacitors of capacitance 2μF and 4μF and a cell of 90 V. The switch 'k' is such that when it is in position 1, the circuit ABCD is closed and when it is in position 2, the circuit BCEF is closed.the resistance of both the circuits is negligible os that the capacitor gets fully charged instantly. Initially the switch is in position1. then it is turned in position 2 and then in position 1. Now two cycles are completed. Find the charge (inμC) after two cycles.
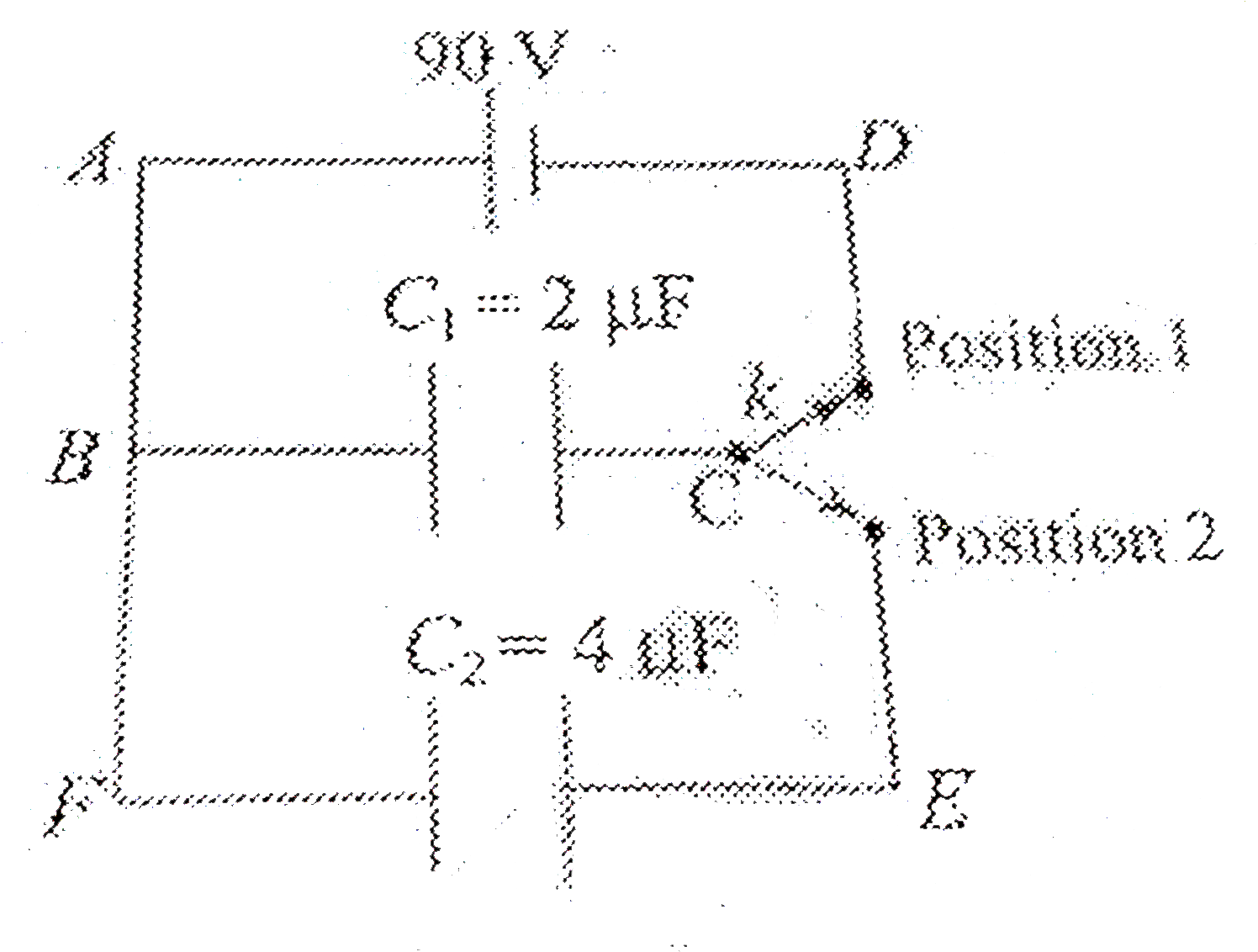
View SolutionFive capacitors each of capacity C are joined as shown in the following figure. If theire resultant capacity CR=2μF, then the capacity of each capacitor is

View SolutionTwo capacitors each of capacity 2μF are connected in parallel. This system is connected in series with a third capacitance of 12μF capacity . The equivalent capacity of the system will be
View SolutionTwo identical capacitors are first connected in series and then in parallel. The difference between their effective capacities is 3μF. The capacity of each capacitor is
View SolutionWhen threee capacitors of equal capacities are connected in parallel and one of the same capacity is connected in series withs its combination . The resultant capacity is 3.75μF. The capacity of each capacitor is
View Solution
