Find the total resistance of a circuit, in which threee resistance are connected in series .
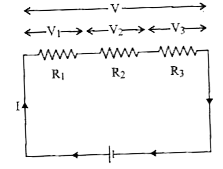
Two or more resistors are said to be connected in series , if the same current is flowing thought each resistor , when some potential differnce is applied across the the combination . Consider three resistors of resistance R1,R2andR3 respectively connected in series . Let I be the current flowing through each resistor . V be the potential differnce each resistor . V be the potential differnce across the series combination .If V1,V2,V3 be the potential difference across the resistors R1,R2andR3 respectively .
V=V1+V2+V3
V=IR1+IR2+IR3
V=I(R1+R2+R3)
If Rs be the effective or equivalent resistance of the series combination , the V=IRs.... (2)
from (1) and (2)
IRS=I(R1+R2+R3)
RS=R1+R2+R3
Similar Questions
Knowledge Check
Total resistance of the circuit:
 A10ΩB20ΩC5ΩD15Ω
A10ΩB20ΩC5ΩD15ΩThere are 8 equal resistances R . Two are connected in parallel, such four groups are connected in series, the total resistance of the system will be
AR/2B2RC4RD8RWhen a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
A700ΩB800ΩC900ΩD100Ω
A galvanometer can be converted into a voltmeter of certain range by connecting a resistance of 880Ω in series with it. When the resistance of 420Ω is connected in series, the range becomes half. Find the resistance of galvanometer.
View SolutionA 24 volt battery is connected to the arrangement of resistances shown in (Fig.) Calculate
(i) the total effective resistance of the circuit,
(ii) the total current flowing in the circuit.
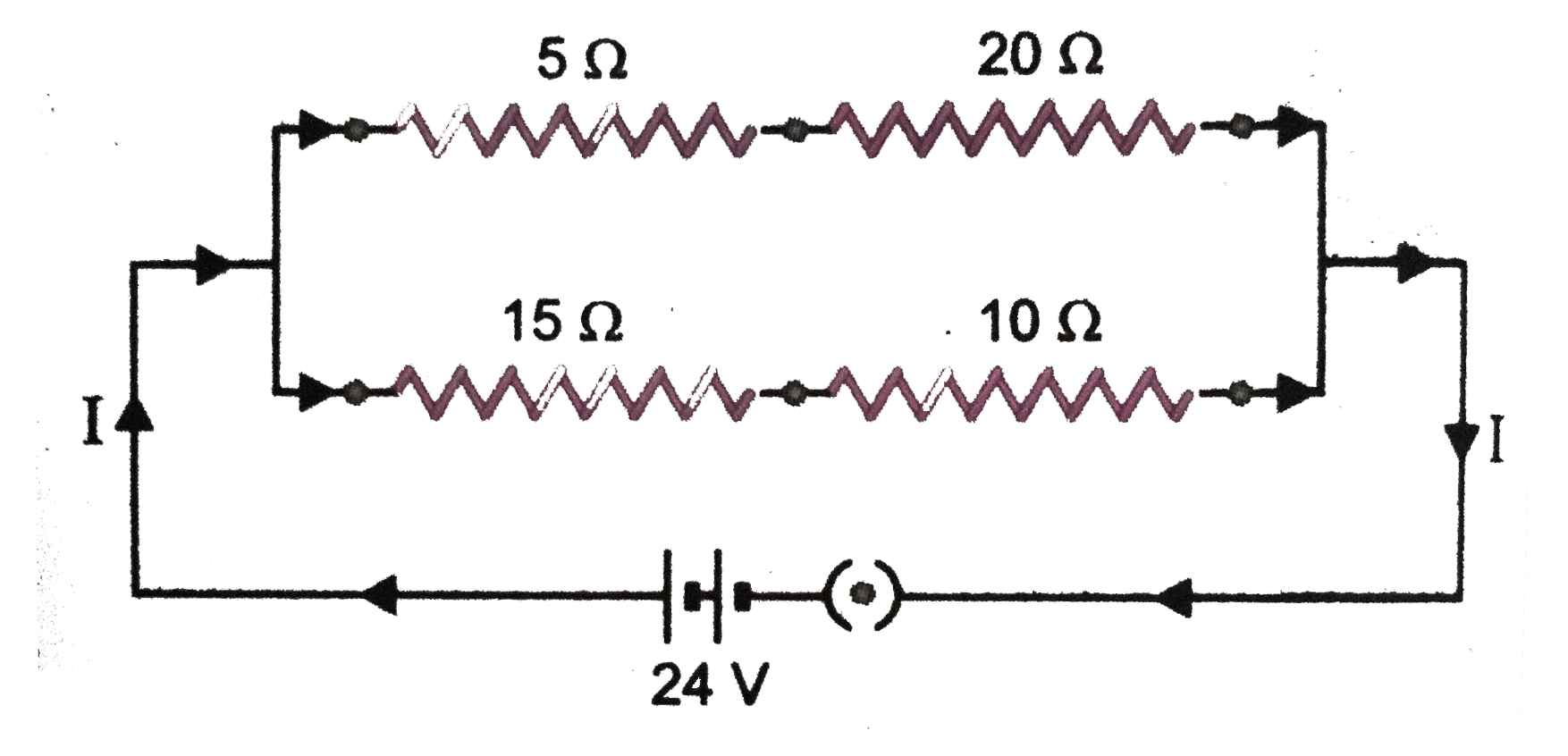 .
.
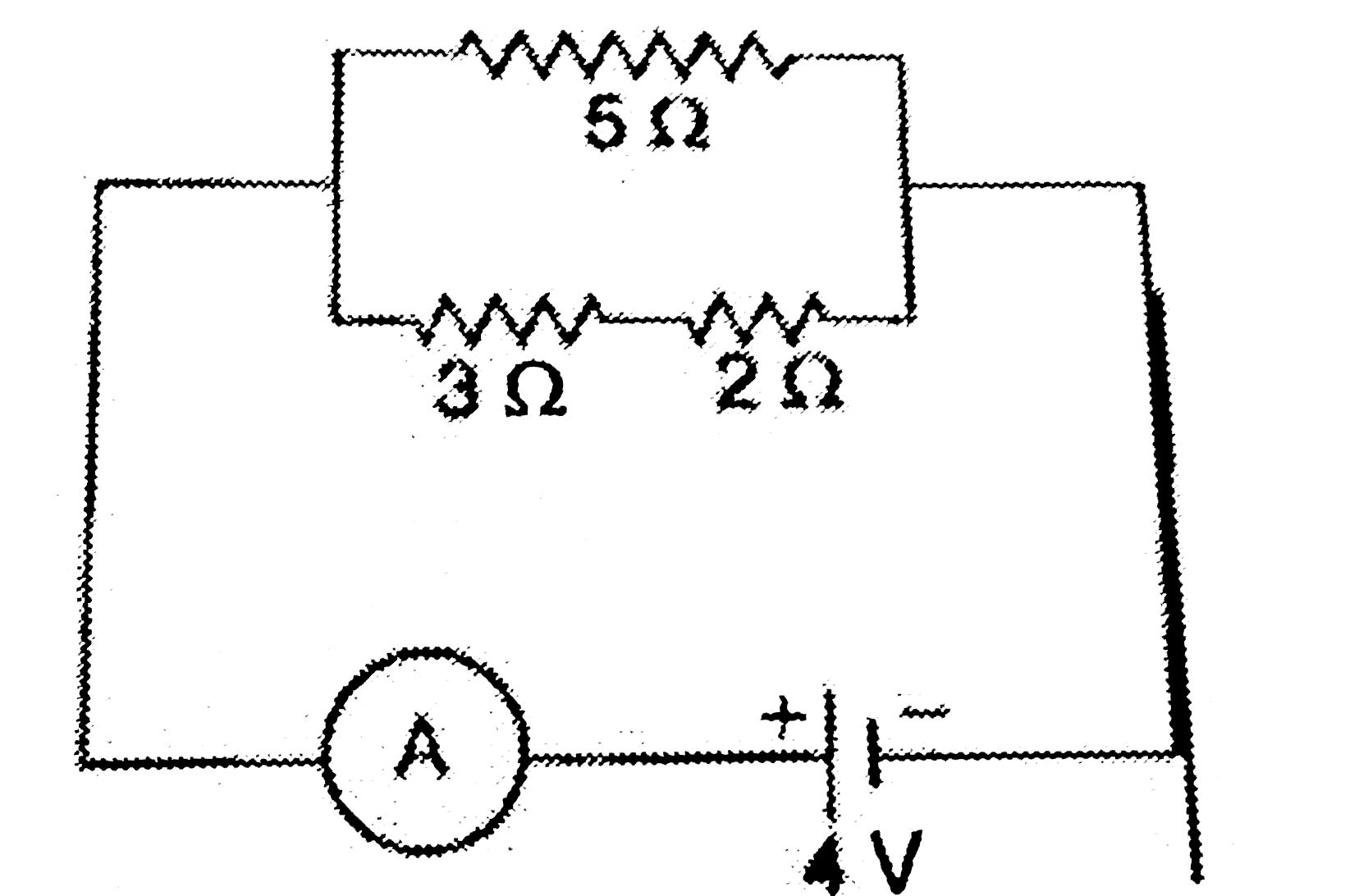
View Solution(a) With the help of a circuit diagram, obtain the relation for the equivalent resistance of two resistances connected in parallel.
(b) In the circuit diagram shown below, find:
(i) Total resistance.
(ii) Current shown by the ammeter A
View SolutionWhen a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
View SolutionWhen a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
View Solution
