A cell of e.m.f . 2 V and internal resistance 0.1Ω is connected to a 3.9Ω external resistance . What will be the potential difference across the terminal of the cell ?

Text Solution
Verified by Experts

Here E=2V
r=0.1Ω
R=3.9Ω
The termimal potential difference is given by
V=ER+rR
=2×3.93.9+0.1
=1.+95V

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12PHYSICSCURRENT ELECTRICITY

Similar Questions

Knowledge Check

  • A cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is

    A1/n
    B1n+1
    Cnn=1
    Dn+1n

  • A cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is

    A(1n)
    B1(n+1)
    Cn(n+1)
    D(n+1)n

  • A cell of emf (E) and internal resistance r is connected across a variable external resistance . R. The graph of terminal potential difference V as a function of R is

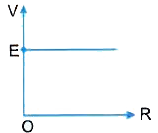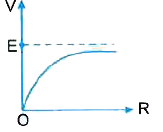    Aocr_image
    Bocr_image
    Cocr_image
    Docr_image