A cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
1/n
1n+1
nn+1
n+1n
The correct Answer is:C
To solve the problem, we need to find the ratio of the terminal potential difference (V) to the electromotive force (E) of a cell connected in series with an external resistance. Here are the steps to derive the solution:
Step 1: Understand the Circuit
We have a cell with an electromotive force (E) and an internal resistance (r). It is connected in series with an external resistance (nr), where n is a constant.
Step 2: Calculate the Total Resistance
The total resistance (R_total) in the circuit is the sum of the internal resistance and the external resistance:
Rtotal=r+nr=r(1+n)
Step 3: Calculate the Current (I)
Using Ohm's Law, the current (I) flowing through the circuit can be calculated using the formula:
I=ERtotal=Er(1+n)
Step 4: Calculate the Terminal Potential Difference (V)
The terminal potential difference (V) can be found using the formula:
V=E−I⋅r
Substituting the expression for I:
V=E−(Er(1+n))⋅r
V=E−E1+n
V=E(1−11+n)
V=E((1+n)−11+n)
V=E(n1+n)
Step 5: Calculate the Ratio of Terminal Potential Difference to E.M.F.
Now, we can find the ratio of the terminal potential difference (V) to the electromotive force (E):
VE=E⋅n1+nE
VE=n1+n
Conclusion
Thus, the ratio of the terminal potential difference to the electromotive force is:
VE=nn+1
Final Answer
The correct answer is nn+1.
We have a cell with an electromotive force (E) and an internal resistance (r). It is connected in series with an external resistance (nr), where n is a constant.
The total resistance (R_total) in the circuit is the sum of the internal resistance and the external resistance:
Rtotal=r+nr=r(1+n)
Using Ohm's Law, the current (I) flowing through the circuit can be calculated using the formula:
I=ERtotal=Er(1+n)
The terminal potential difference (V) can be found using the formula:
V=E−I⋅r
Substituting the expression for I:
V=E−(Er(1+n))⋅r
V=E−E1+n
V=E(1−11+n)
V=E((1+n)−11+n)
V=E(n1+n)
Now, we can find the ratio of the terminal potential difference (V) to the electromotive force (E):
VE=E⋅n1+nE
VE=n1+n
Thus, the ratio of the terminal potential difference to the electromotive force is:
VE=nn+1
The correct answer is nn+1.
Similar Questions
A cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View SolutionA cell of e.m.f E and internal resitance r ,is connected to an external resistance R. the variation of potential difference V across the resistance R as function of R as shown in the figure, is the best represented by curve
_PHY_E01_011_Q01.png)
View Solution
Knowledge Check
A cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
A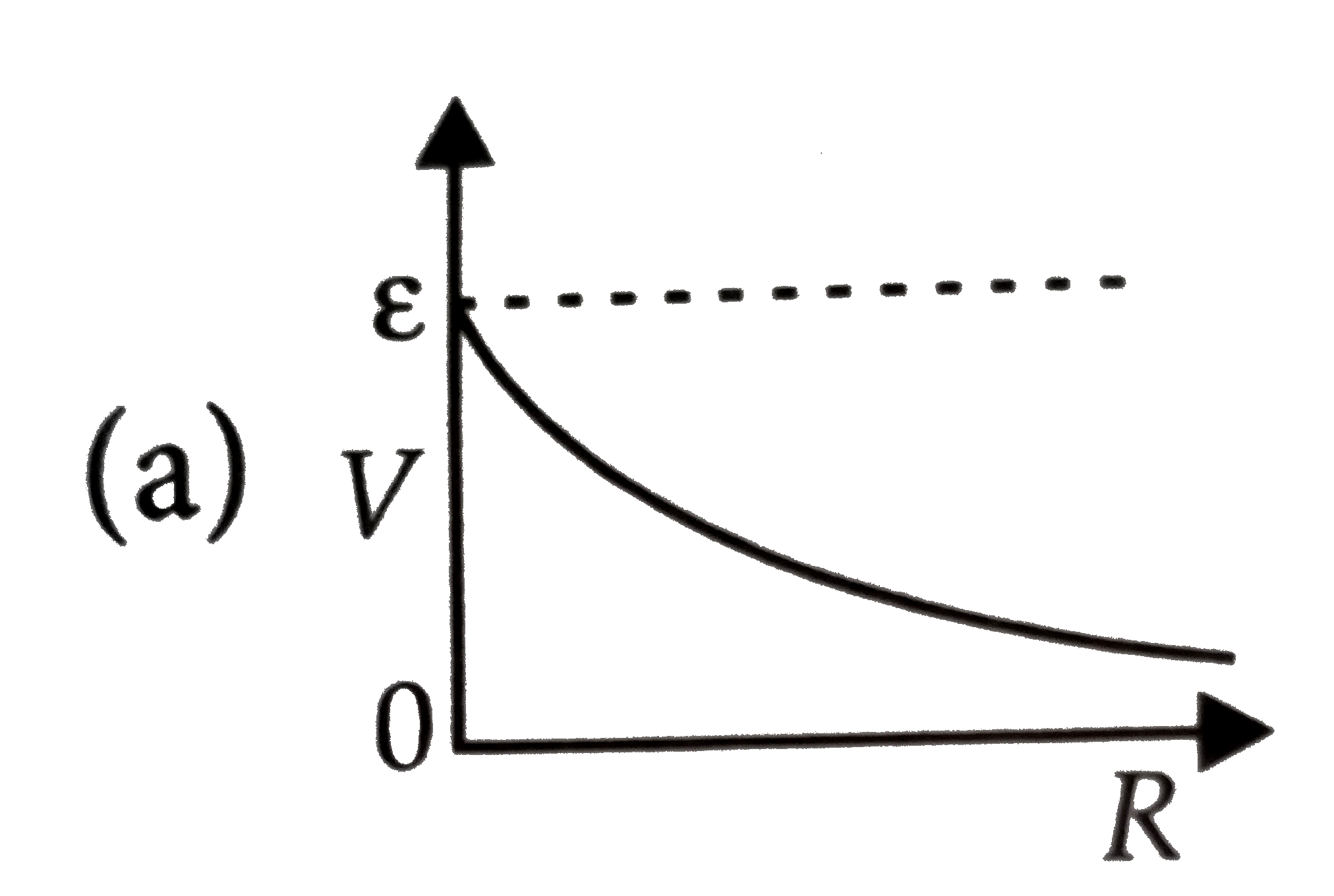 B
B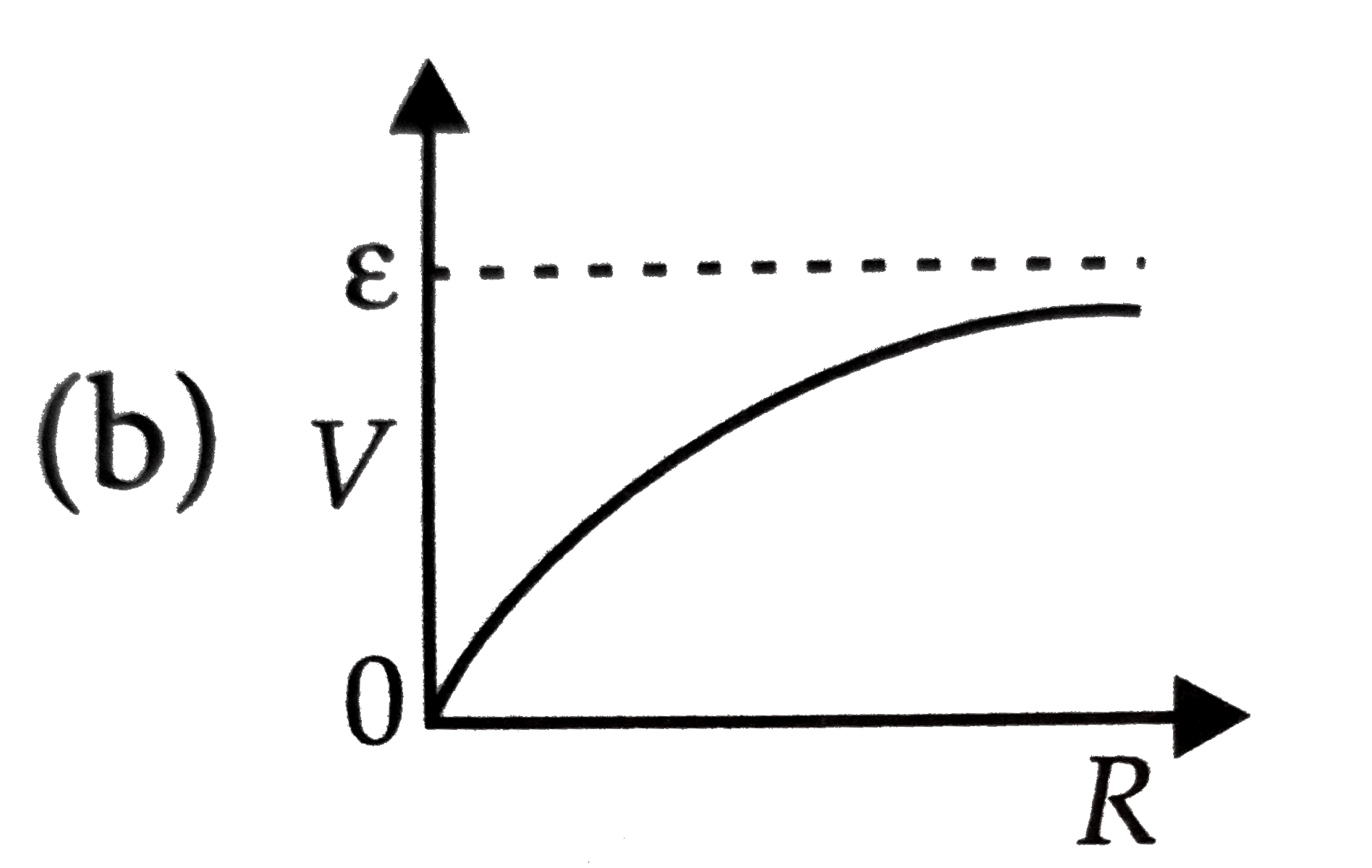 C
C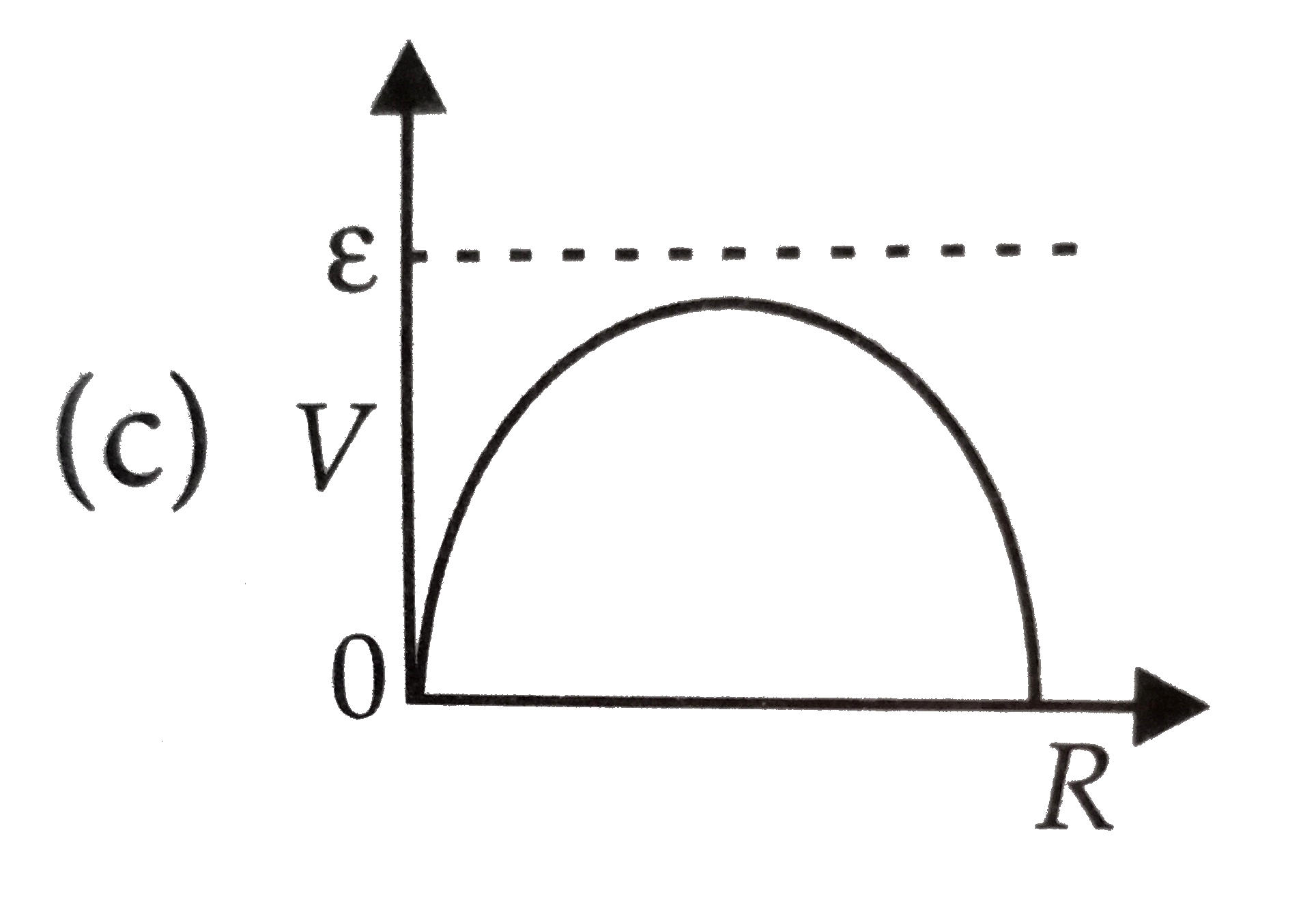 D
D
A cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionThere are n cells, each of emf E and internal resistance r, connected in series with an external resistance R. One of the cells is wrongly connected, so that it sends current in the opposite direction. The current flowing in the circuit is
View SolutionA cell of e.m.f. 'E' and internal resistance 'r' is connected across a variable resistor 'R'. Plot a graph showing the variation of terminal potential 'V' with resistance R.
Predict from the graph the condition under which 'V' becomes equal of 'E'

View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionA cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig. What is the potential difference across the terminals of the cell ?
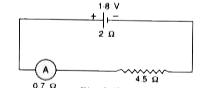
View SolutionA cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
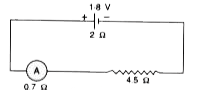
What would be the reading of the ammeter ?
View Solution
