A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius.. Find the volume of the solid in terms of π.Solution in Punjabi
The correct Answer is:πcm3
Step by step video, text & image solution for A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius.. Find the volume of the solid in terms of pi. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SURFACE AREAS AND VOLUME Book:NAND LAL PUBLICATIONChapter:SURFACE AREAS AND VOLUME Exercise:EXERCISE 13.3
Explore 9 Videos
- SURFACE AREAS AND VOLUME Book:NAND LAL PUBLICATIONChapter:SURFACE AREAS AND VOLUME Exercise:EXERCISE 13.4
Explore 5 Videos
- SURFACE AREAS AND VOLUME Book:NAND LAL PUBLICATIONChapter:SURFACE AREAS AND VOLUME Exercise:EXERCISE 13.5
Explore 7 Videos
- QUADRATIC EQUATIONS Book:NAND LAL PUBLICATIONChapter:QUADRATIC EQUATIONS Exercise:EXERCISE 4.4
Explore 8 Videos
- TRIANGLES Book:NAND LAL PUBLICATIONChapter:TRIANGLES Exercise:EXERCISE 6.6
Explore 11 Videos
Similar Questions
A metallic sphere of radius 4.2 cm is melted and recast into the shape of cylinder of radius 6 cm. Find the height of the cylinder.
View SolutionA drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
View SolutionA copper wire 3 mm in diameter is wound about a cylinder whose length is 12 cm, and diameter 10 cm,so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to 8.88 g per cm3.
View SolutionFind the nature of the roots of the following quadratic equations. If the real roots exist, find them :- 2x2−3x+5=0 .
View SolutionIn figure , D is point on hypotenuse AC of ΔABC,BD⊥AC,DM⊥BCandDN⊥AB. Prove that
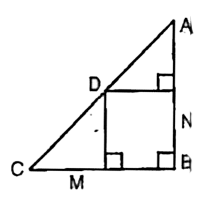
DM2=DN.MC
View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π
View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π .
View SolutionA solid is in the form of a cone standing on a hemisphere with both their radii being equal to 8 cm and the height of cone is equal to its radius . Find the volume of solid.
View Solutionएक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिनकी त्रिज्याएँ 1 सेमी है तथा शंकु की ऊँचाई उसकी त्रिज्या के बराबर है | इस ठोस का आयतन π के पदों में ज्ञात कीजिए |
View Solutionएक ठोस एक शंकु के आकार का है जो कि एक अर्धगोले पर रखा हुआ है और दोनों की त्रिज्याएँ 1 सेमी हैं तथा शंकु की ऊँचाई इसकी त्रिज्या के बराबर है। इस ठोस का आयतन तथा पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
View Solutionएक ठोस एक अर्द्धगोले के ऊपर समान त्रिज्या 8 सेमी के शंकु के रूप में है और शंकु की ऊंचाई इसकी त्रिज्या के बराबर है ठोस का आयतन ज्ञात कीजिए ।
View Solutionएक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिसकी त्रिज्याएँ 1 सेमी है तथा शंकु की ऊंचाई उसकी त्रिज्या के बराबर है । इस ठोस का आयतन π के पदों में ज्ञात कीजिए ।
View SolutionA solid sphere of radius r melted and recast into the shape of a solid cone of height r, then radius of the base of the cone is (of equal volume)
View SolutionA solid in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
View SolutionA solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius.. Find the volume of the solid in terms of π.
View Solution