The fraction of gaseous molecules having speed in between u and u+ du as governed by Maxwell distribution of speeds is given by dNuN=4π(M2πRT)1/2 exp (−Mu2/2RT)u2 du
Graphically this distribution is shown in fig.
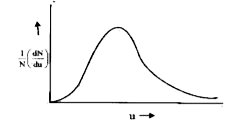
Based on this distribution, answer the following three question
With increase in temperature, the quantity (dN/N)/du in the high speed range Solution in Malayalam
increases
decreases
shows no change
increases or decreases depending upon the gas
The correct Answer is:A
In the high speed range , the reverse of the effects discussed in (i) is observed , consequently the fraction increases.
Topper's Solved these Questions
- BOOK - BRILLIANT PUBLICATIONCHAPTER - STATES OF MATTER EXERCISE - LEVEL III (Statement Type )5videos
STATES OF MATTER
- BOOK - BRILLIANT PUBLICATIONCHAPTER - SOME BASIC CONCEPTS OF CHEMISTRYEXERCISE - LEVEL-I55videos
SOME BASIC CONCEPTS OF CHEMISTRY
- BOOK - BRILLIANT PUBLICATIONCHAPTER - STRUCTURE OF ATOMSEXERCISE - LEVEL - III (Linked Comprehension Type)8videos
STRUCTURE OF ATOMS
Similar Questions
Assertion : Ideal gas equation is nearly valid for real gases at low pressure and high temperature.
Reason : Molecular interactions are negligible under this condition.03:06View SolutionWhich of the following is a characteristic of both mixtures and compounds?
01:05View SolutionThe hydrogen-like species Ļi2+ is in a spherically symmetric state S1 with one radial node. Upon absorbing light the ion undergoes transition to a state S2 The state S2 has one radial node and its energy is equal to the ground state energy of the hydrogen atom.
The state S1 is: 1s, 2s, 2p, 3s01:49View SolutionIf u=ax+b,thendndxn(f(ax+b)) is equal to a.dndun(f(u)) b. adndun(f(u)) c. andndunf(u) d. a−ndndxn(f(u))
04:00View Solutionint (du) / (u sqrt (u ^ (2) -1))
06:40View SolutionSuppose an object has thickness du so that it extends from object distance u to u+du. Prove that the thickness dv of its image is given by (−v2u2)du, so the longitudinal magnification dvdu=−m2, where m is the lateral magnification.
03:54View SolutionA hypothetical gas sample has its molecular speed distribution graph as shown in the figure. The speed (u) and dNdu have appropriate units. Find the root mean square speed of the molecules. Do not worry about units.
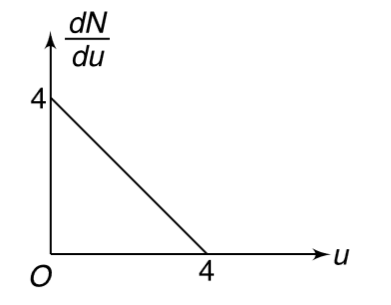 00:47View Solution
00:47View SolutionThe speed distribution of molecules in a sample of a gas is shown in the figure. The graph between dNdu and u is a parabola and total number of molecules in the sample is N0.
(a) Calculate the rms speed of the molecules.
(b) Calculate the total translational kinetic energy of molecules if mass of the sample is 10 g.
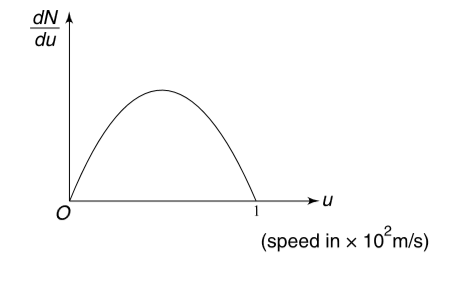 06:47View Solution
06:47View Solutionint_(2)^(3)u sqrt(5-u)du
04:52View Solution∫1√udu
02:54View Solution∫tan−1u(1+u)2du
03:03View SolutionIf ∫x0{∫u0f(t)dt}du is equal to (a) ∫x0(x−u)f(u) (b) ∫x0uf(x−u)du (c) x∫x0f(u)du (d) x∫x0uf(u−x)du
03:20View Solution∫x0{∫u0f(t)dx} du is equal to (a) ∫x0(x−u)f(u)du (b) ∫x0uf(x−u)du (c) x∫x0f(u)du (d) x∫x0uf(u−x)du
04:35View SolutionSuppose an object has thickness du so that it extends from object distance u to u+du. Prove that the thickness dv of its image is given by (-v^2/u^2)du, so the longitudinal magnification (dv)/(du)=-m^2, where m is the lateral magnification.
04:44View SolutionIf u=t2andv=sint2then dv/du=________.
02:56View SolutionA hypothetical gas sample has its molecular speed distribution graph as shown in the figure. The speed (u) and dNdu have appropriate units. Find the root mean square speed of the molecules. Do not worry about units.
 04:16View Solution
04:16View Solution

