The fraction of gaseous molecules having speed in between u and u+ du as governed by Maxwell distribution of speeds is given by dNuN=4π(M2πRT)1/2 exp (−Mu2/2RT)u2 du
Graphically this distribution is shown in fig.

Based on this distribution, answer the following three question
The maximum value of (dN/N)/du corresponds to most probable speed. With increase in temperature, this maximum fractionSolution in Malayalam
increases
decreases
shows no change
increases or decreases depending upon the gas
The correct Answer is:B
Here , also fraction decreases .
Topper's Solved these Questions
- STATES OF MATTER BOOK - BRILLIANT PUBLICATIONCHAPTER - STATES OF MATTER EXERCISE - LEVEL III (Statement Type )
5 Videos
- SOME BASIC CONCEPTS OF CHEMISTRYBOOK - BRILLIANT PUBLICATIONCHAPTER - SOME BASIC CONCEPTS OF CHEMISTRYEXERCISE - LEVEL-I
55 Videos
- STRUCTURE OF ATOMSBOOK - BRILLIANT PUBLICATIONCHAPTER - STRUCTURE OF ATOMSEXERCISE - LEVEL - III (Linked Comprehension Type)
8 Videos
Similar Questions
Assertion : Ideal gas equation is nearly valid for real gases at low pressure and high temperature.
Reason : Molecular interactions are negligible under this condition.
View SolutionWhich of the following is a characteristic of both mixtures and compounds?
View SolutionThe hydrogen-like species Ļi2+ is in a spherically symmetric state S1 with one radial node. Upon absorbing light the ion undergoes transition to a state S2 The state S2 has one radial node and its energy is equal to the ground state energy of the hydrogen atom.
The state S1 is: 1s, 2s, 2p, 3s
View SolutionIf u=ax+b,thendndxn(f(ax+b)) is equal to a.dndun(f(u)) b. adndun(f(u)) c. andndunf(u) d. a−ndndxn(f(u))
View Solutionint (du) / (u sqrt (u ^ (2) -1))
View SolutionSuppose an object has thickness du so that it extends from object distance u to u+du. Prove that the thickness dv of its image is given by (−v2u2)du, so the longitudinal magnification dvdu=−m2, where m is the lateral magnification.
View SolutionA hypothetical gas sample has its molecular speed distribution graph as shown in the figure. The speed (u) and dNdu have appropriate units. Find the root mean square speed of the molecules. Do not worry about units.
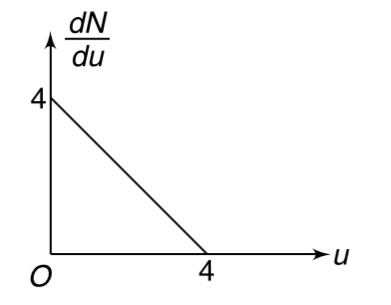
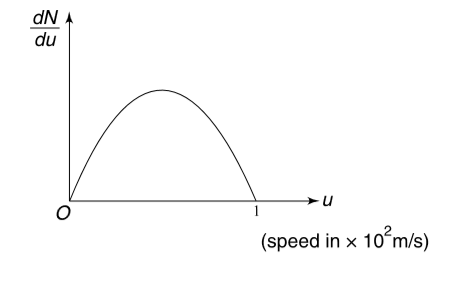
View SolutionThe speed distribution of molecules in a sample of a gas is shown in the figure. The graph between dNdu and u is a parabola and total number of molecules in the sample is N0.
(a) Calculate the rms speed of the molecules.
(b) Calculate the total translational kinetic energy of molecules if mass of the sample is 10 g.
View Solutionint_(2)^(3)u sqrt(5-u)du
View Solution∫1√udu
View Solution∫tan−1u(1+u)2du
View SolutionIf ∫x0{∫u0f(t)dt}du is equal to (a) ∫x0(x−u)f(u) (b) ∫x0uf(x−u)du (c) x∫x0f(u)du (d) x∫x0uf(u−x)du
View Solution∫x0{∫u0f(t)dx} du is equal to (a) ∫x0(x−u)f(u)du (b) ∫x0uf(x−u)du (c) x∫x0f(u)du (d) x∫x0uf(u−x)du
View SolutionSuppose an object has thickness du so that it extends from object distance u to u+du. Prove that the thickness dv of its image is given by (-v^2/u^2)du, so the longitudinal magnification (dv)/(du)=-m^2, where m is the lateral magnification.
View SolutionIf u=t2andv=sint2then dv/du=________.
View SolutionA hypothetical gas sample has its molecular speed distribution graph as shown in the figure. The speed (u) and dNdu have appropriate units. Find the root mean square speed of the molecules. Do not worry about units.

View Solution
