ABC is a right angled triangle of which A is the right angle, BD is drawn perpendicular to BC and meets CA produced in D. If AB = 12, AC = 16, BC = 20, then BD=
15
25
10
225
The correct Answer is:A
Similar Questions
Knowledge Check
ABC is a right angled triangle of which A is the right angle, BD is drawn perpendicular to BC meets CA produced in D. If AB = 12, AC = 16, BC = 20, then BD =
A15B25C10D225
ΔABC is a right angle triangle (right angled at B), BD is perpendicular to AC. If AC=16cmBC=9cm, find the length of CD.
View SolutionABC is right angle triangle where AD is perpendicular on hypotenuse BC. If AC = 2 AB find BD.
View SolutionΔABC is a right angle triangle (right angled at B), BD is perpendicular to AC. If AC = 16 cm, BC = 12 cm, find the length of CD.
View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
AB2−BD2=AC2−CD2
View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
AB2−BD2=AC2−CD2
View SolutionABC is right triangle right angled at B.If BD is the length of the perpendicular drawn from B to AC then
View SolutionIn the figure given below , ABC is right angled at B and ΔABD is right angled at A. If BD is perpendicular to AC and BC=2√3 cm with ∠CAB=30∘, then the length of AD is___
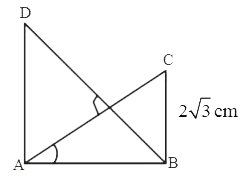
View Solution
