If the areas of I-II hysteresis loop and B-H hysterisis loop are denoted by A1andA2, then
A2=μ0A1
μ∝1n
μ∝n2
μ∝1n2
The correct Answer is:A
In S.I. units, →B=μ0(→H+→I)
∴dB=μ0dH=μ0dI ∴∮.dB=μ0∮H.dH+μ0∮HdI
As ∮H.dH=0 ∴∮H.dB=μ0∮H.dI
i.e., are of BH loop =μ0× are of I-H loop
A2=μ0A1
Similar Questions
Knowledge Check
- Question 1 - Select One
If the areas under the I−H hysteresis loop and BH hysteresis loop are denoted by A1 and A2, then
AA2=μ0A1BA2=A1CA2=A1μ0DA2=μ20A1 - Question 2 - Select One
The area enclosed by a hysteresis loop is a measure of
AretentivityBsusceptibilityCpermeabilityDenergy loss per cycle - Question 3 - Select One
A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
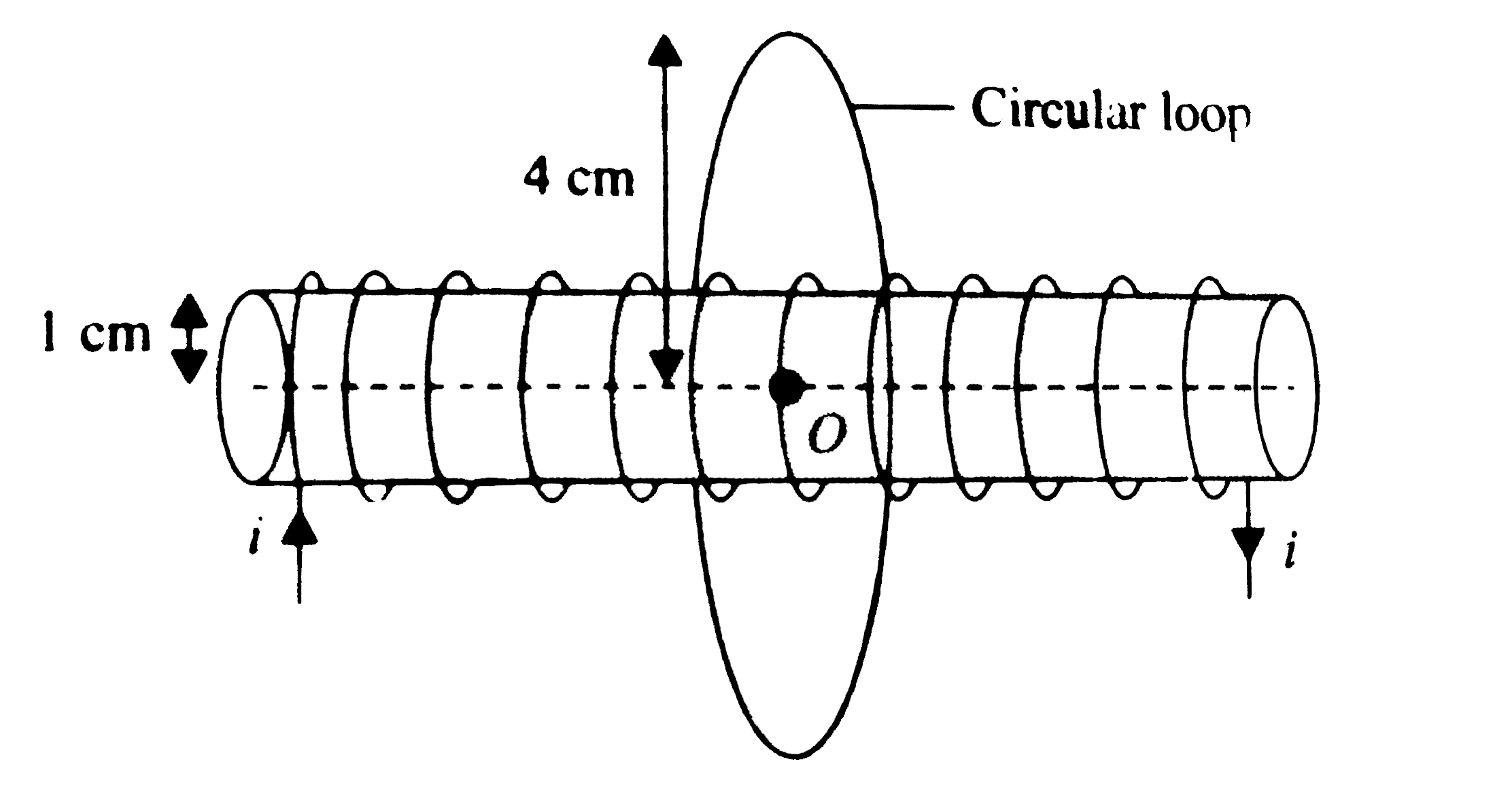
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoidAμ0ni(πa21)Bμ0ni(πa22)CzeroDμ0ni(πa21+πa22)
A long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoidView SolutionLet A1,A2,A3,A4 be the areas of the triangular faces of a tetrahedron, and h1,h2,h3,h4 be the corresponding altitudes of the tetrahedron. If the volume of tetrahedron is 16 cubic units, then find the minimum value of (A1+A2+A3+A4)(h1+h2+h3+h4) (in cubic units).
View Solution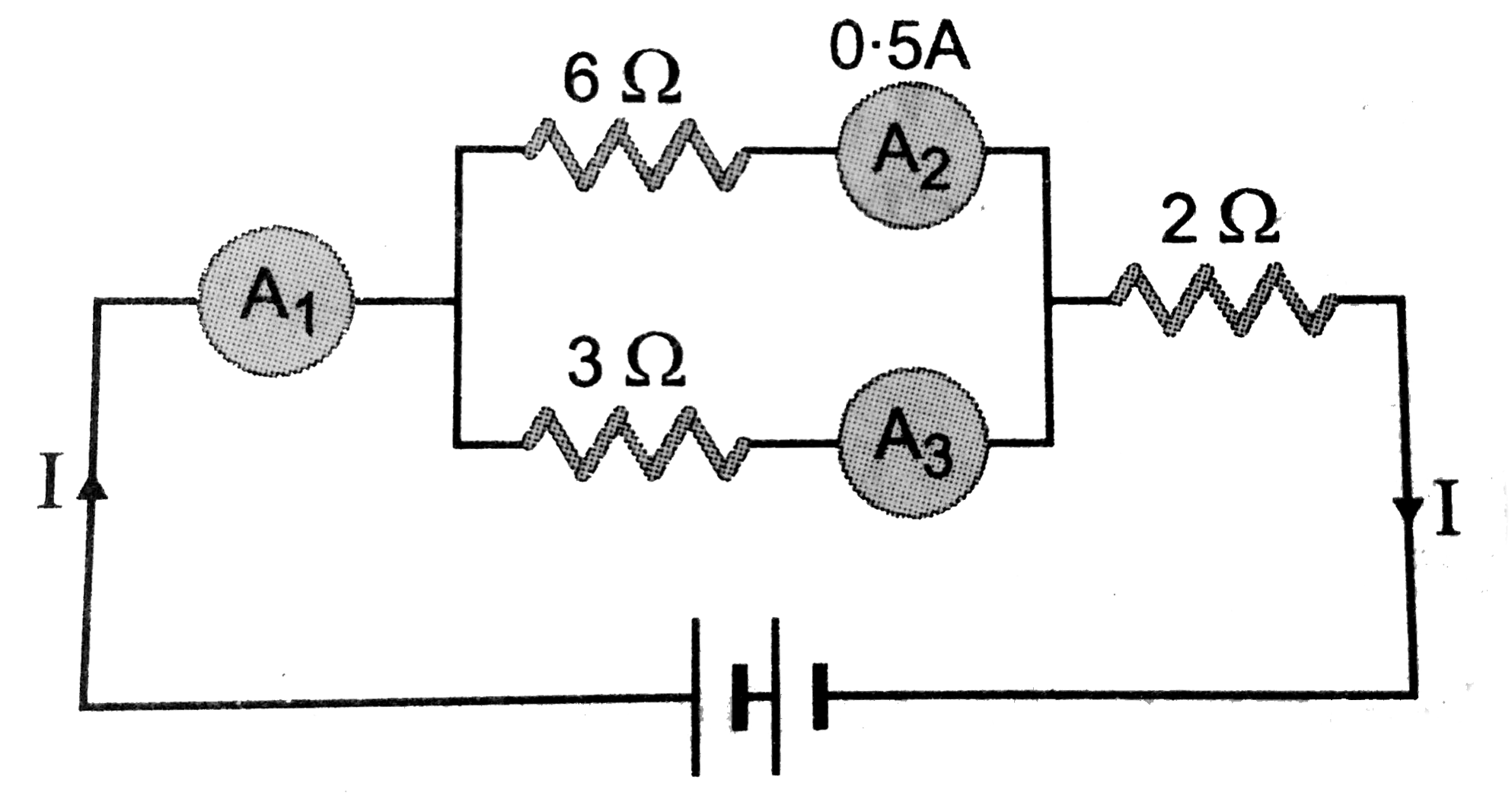
A1,A2andA3 Are the ammeters and A2 reads 0.5A. (i) What are the readings of ammeters A1 and A3 ? (ii) What is the total resistance of the circuit ?View SolutionIf A1 denotes area of the region bounded by the curves C1:y=(x−1)ex tangent to C1 at (1,0) & y-axis and A2 denotes the area of the region bounded by C1 and co-ordinate axes in the fourth quadrant then (A) A1>A2 (B) A1<A2 (C) 2A1+A2=2 (D) A1+2A2=4
View SolutionLet a1,b1=8,a1+1=a1+32b1 and b1+1=12b1∀I=1,2,3…… Let Ai be area of the loop formed by |x−a1|+|y|=b1. If all the loops are plotted on the same X-Y plane, then the value of ∪A1 is
View Solution

