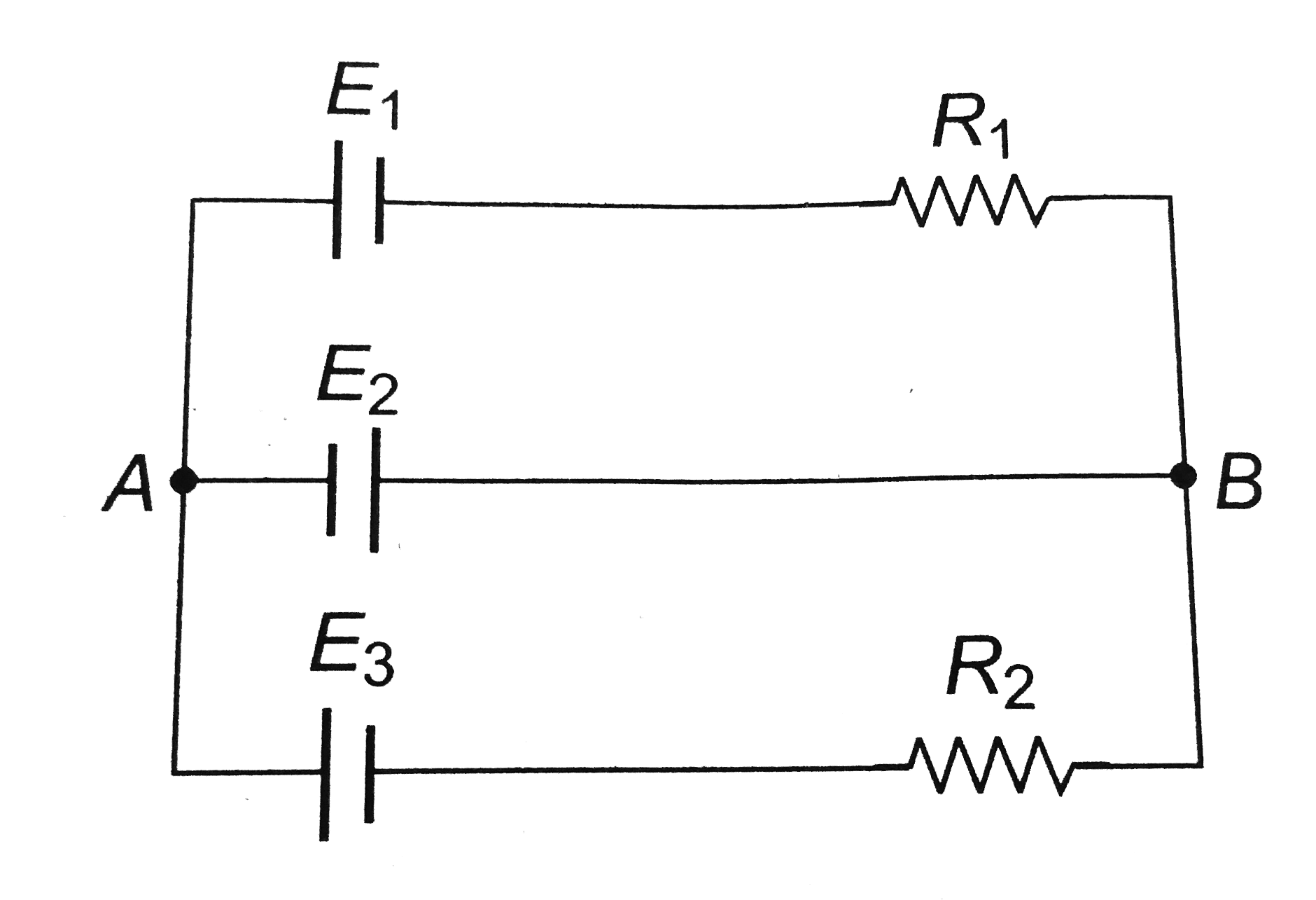
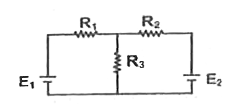
In the circuit shown in the Fig., E1=E2=E3=2V and R1=R2=4Ω. The current flowing between points A and B through battery E2 is:
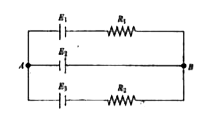
zero
2A from A to B
2A from B to A
none of the above
The correct Answer is:B
For loop (1) 2+2−4I1=0 or i1=1A
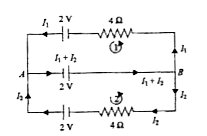
For loop (2), −2−2+4I2=0 or I2=1A
So the current from A to B is I1+I2=2A
Similar Questions
Knowledge Check
In the circuit shown in fig. 5.265, E1=E2=E3=2V and R1=R2=4Ω. The current flowing between points A and B through battery E2 is
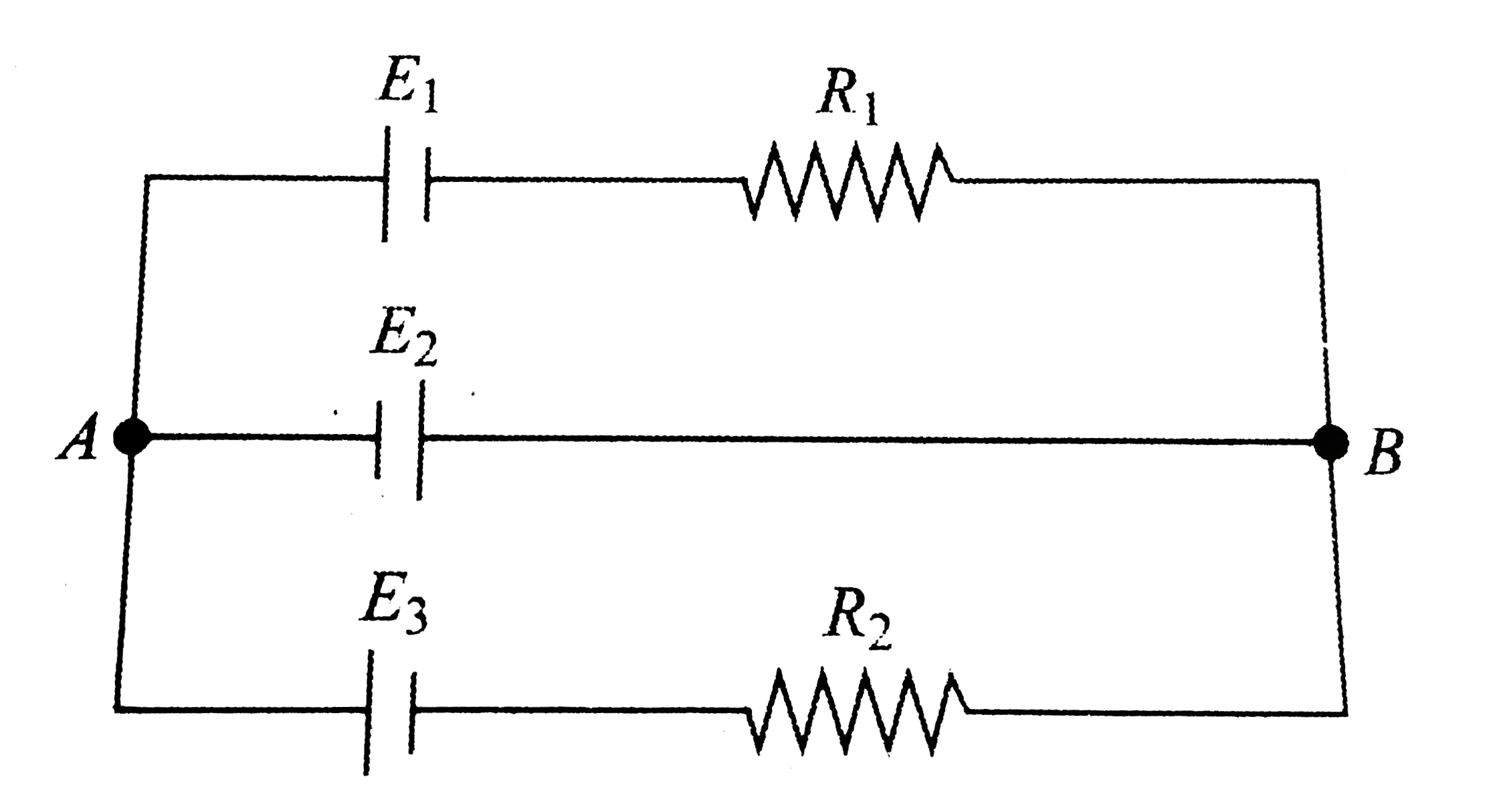 AzeroB2 A from A to BC2 A form B to ADnone of the above
AzeroB2 A from A to BC2 A form B to ADnone of the aboveIn the circuit shown here, E1=E2=E3=2V and R1=R2=4ohms. The current flowing between point A and B through battery E2 is
 AZeroB2amp from A to BC2amp from B to ADNone of the above
AZeroB2amp from A to BC2amp from B to ADNone of the aboveIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3
 Ai=0Bi=2ACV=14VDV=7V
Ai=0Bi=2ACV=14VDV=7V
In the following circuit E1=E2=E32V and R1=R2=AΩ. The current passing through battery E2 between points A and B is
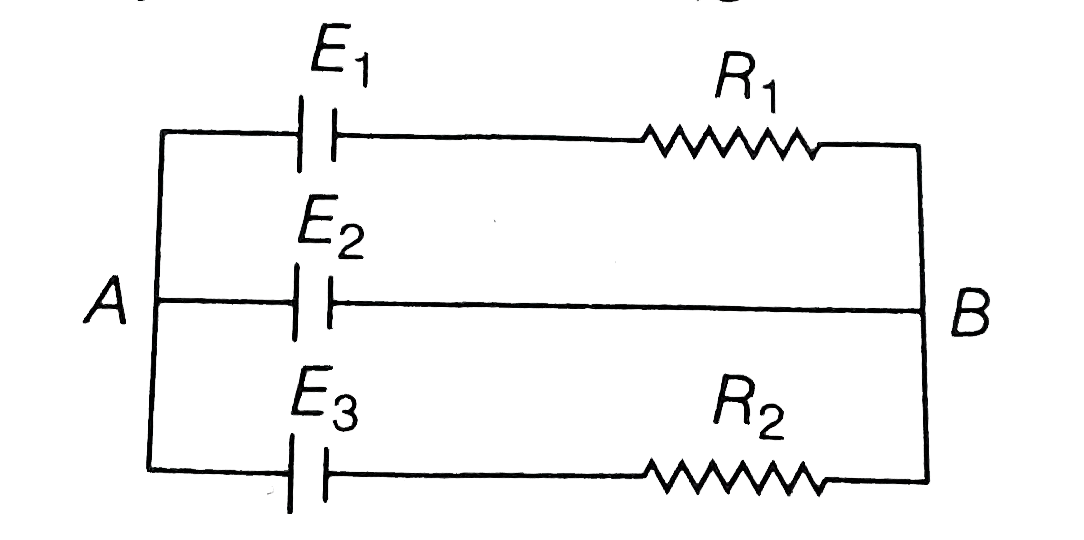
View SolutionIn the circuit as shown in figure,
E1=2V,E2=2V,E3=1V,andR=r1=r2=r3Ω.
The potential difference between points A and B will be

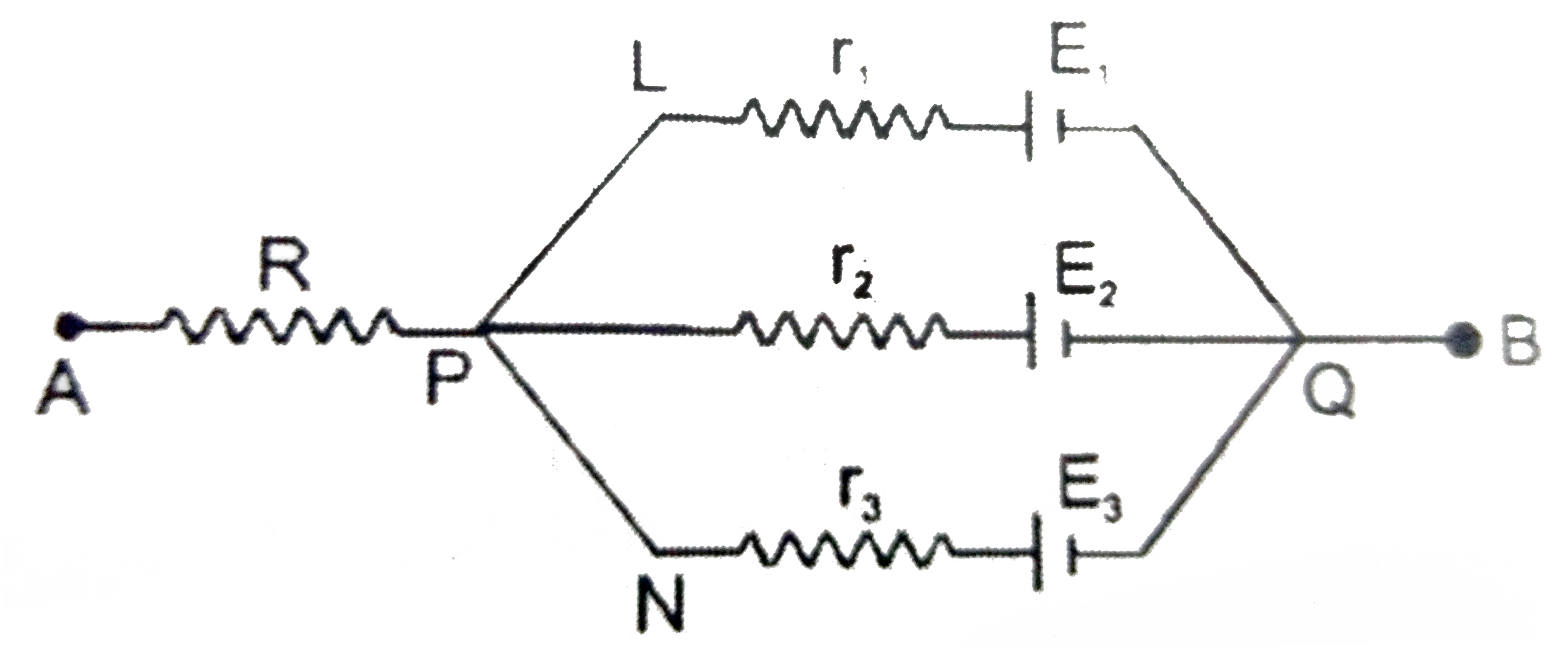
View SolutionIn the circuit shown in figure ,(ε)1=3V,(ε)2=2V,(ε)3=1Vandr1=r2=r3=1(Ω).Find the potential difference between the points A and B and the current through each branch.

View SolutionIn the circuit shown in fig. E1=3 volt,E2=2 volt,E3=1 vole and R=r1=r2=r3=1ohm.
(i) Find potential difference in Volt between the points A and B with A & B unconnected.
(ii) If r2 is short circuited and the point A is coneted to point B through a zero resistance wire, find the current through R in ampere.
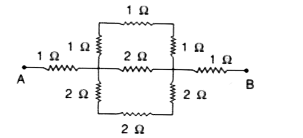
View SolutionCalculate the effective resistance between the points A and B in the circuit shown in Fig.
View Solution
