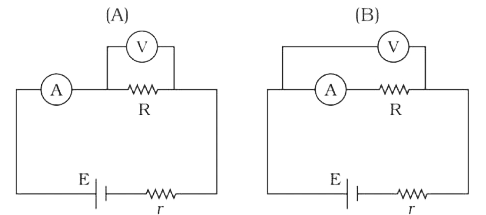
Resistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (Rv and RG respectively) are finite and non-zero.

Let RA and RB be the calculated values in the two cases (a) and (b) respectively.
If the resistance of voltmeter is Rv=1Ω , and that of ammeter is RG=1Ω, the magnitude ofthepercentage error in the measurement of R (the value of R? is nearly 10Ω) is:
zero in both cases
non-zero but equal in both cases
more in circuit A
more in circuit B
The correct Answer is:D
% error in case A.
RA−RR×100=(RVR+RV−1)×100=−RR+RV×100=−1%
% error in case B RB−RR×10=RGR×100=10%
Similar Questions
Resistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRGrespectively ) are finite and non zero.

Let RvandRG be the calculated values in the two cases A and B respectively.
If the resistance of voltmeter is Rv=1kΩ and that of ammeter is RG=1Ω the magnitude of the percentage error in the measurement of R (the value of R is nearly 10Ω ) is:View SolutionResistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRGrespectively ) are finite and non zero.
Let RvandRG be the calculated values in the two cases A and B respectively.
The relation between RBand the actual value of R is:View Solution
Knowledge Check
- Question 1 - Select One
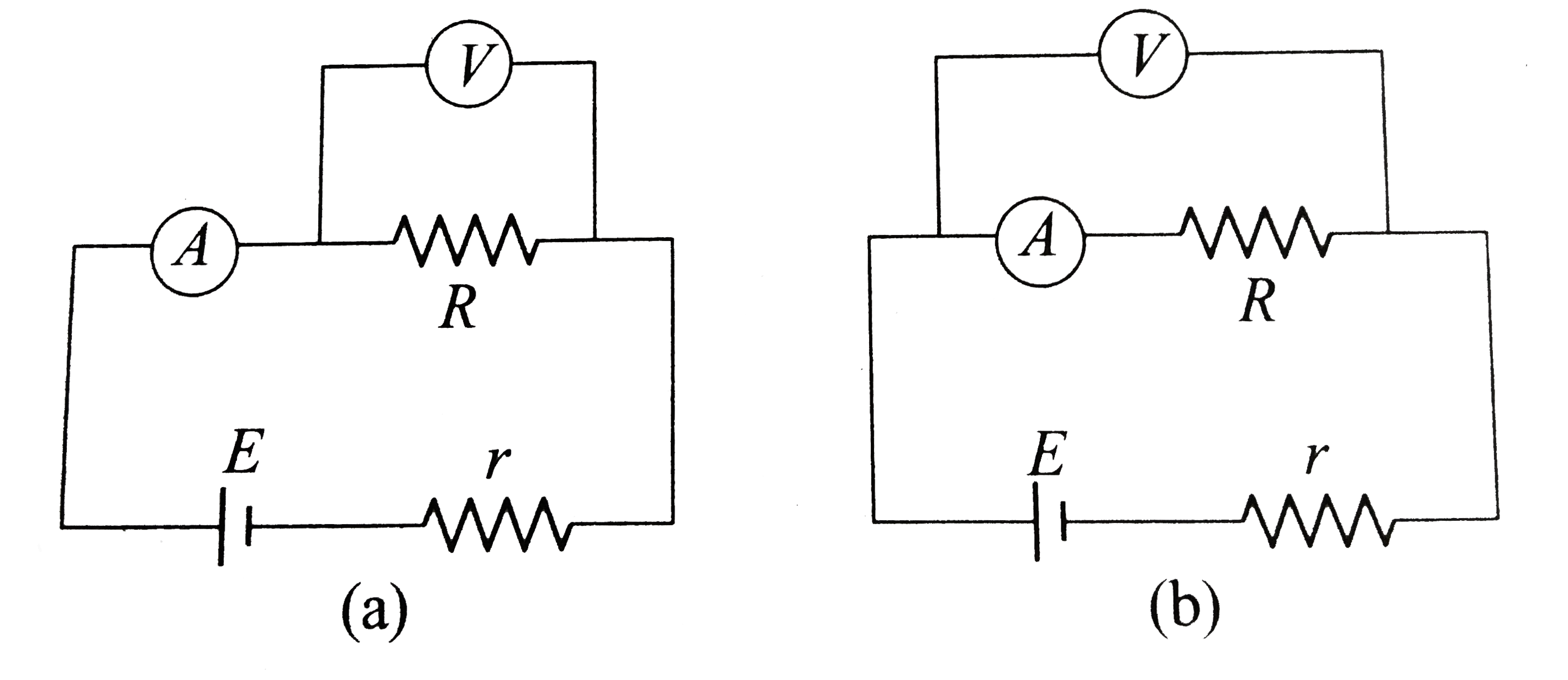
The value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
The relation between RA and the actual value of R isAR>RABR<RACR=RBDdependent upon E and r. - Question 2 - Select One
The value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
If the resistance of voltmeter is RV=1kΩ and the percentage error in the measurement of R (the value of R is nearly 10Ω)isAzero in both casesBnonzero but equal in both casesCmore in circuit ADmore in circuit B - Question 3 - Select One
Let V and I be the readings of the voltmeter and the ammeter respectively as shown in the figure. Let RV and RA be their corresponding resistancce Therefore,
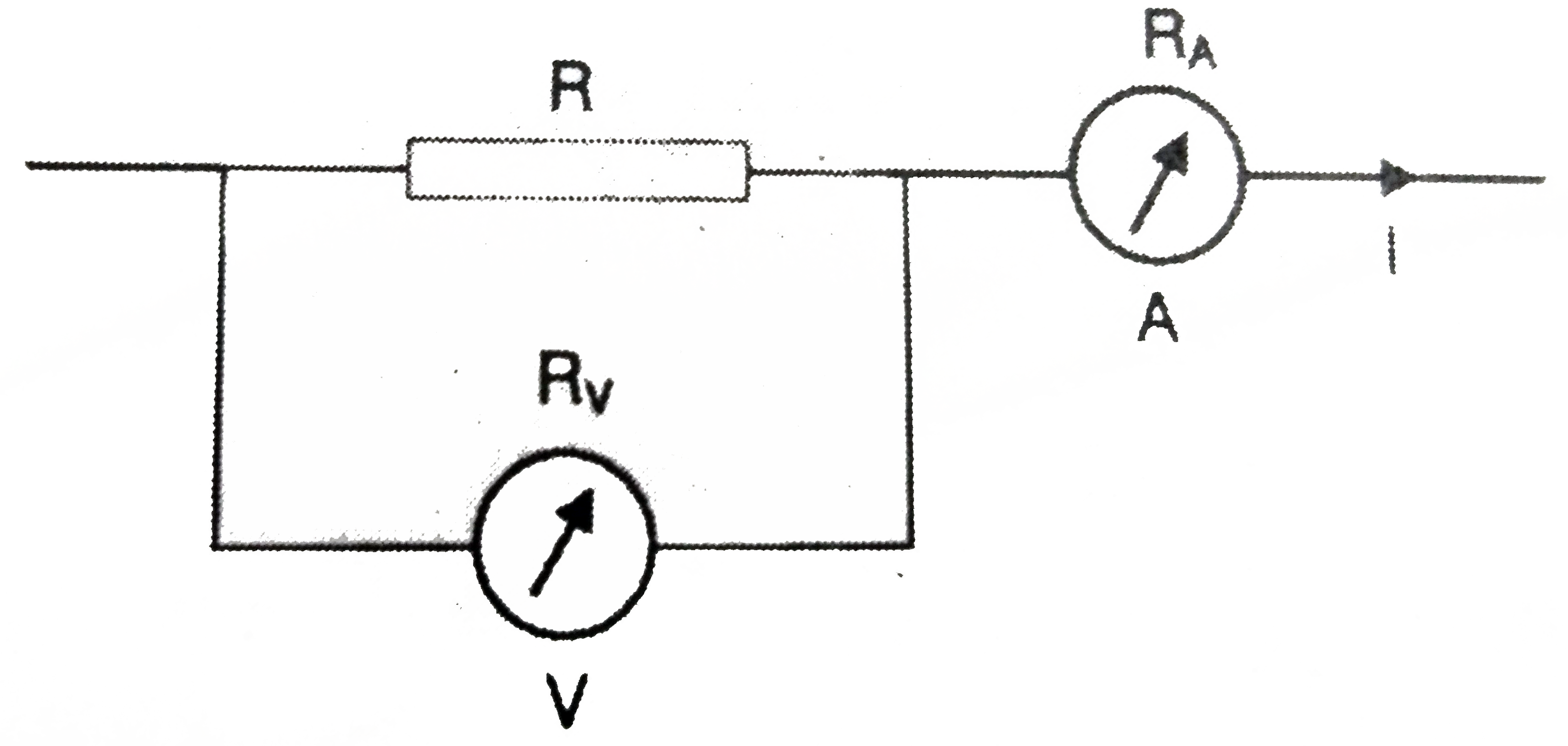 AR=VIBR=VI−(VRV)CR=RV−RADR=V(R+RA)IRA
AR=VIBR=VI−(VRV)CR=RV−RADR=V(R+RA)IRA
Resistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRBrespectively ) are finite and non zero.
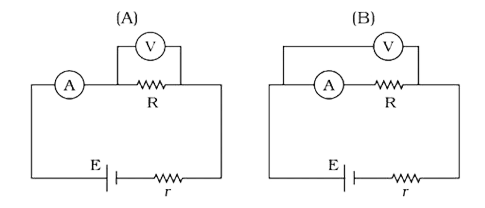
Let RAandRB be the calculated values in the two cases A and B respectively.
The relation between RA and the actual value R isView SolutionThe value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
If the resistance of voltmeter is RV=1kΩ and the percentage error in the measurement of R (the value of R is nearly 10Ω)isView SolutionLet V and I be the readings of the voltmeter and the ammeter respectively as shown in the figure. Let RV and RA be their corresponding resistancce Therefore,
 View Solution
View SolutionIn the series L-C-R circuit , the voltmeter and ammeter readings are respectively
 View Solution
View SolutionIf resistance of voltmeter is 10000Ω and resistance of ammeter is 2Ω then find R when voltmeter reads 12 V and ammeter reads 0.1 A
View Solution

