P=b2c2−ac−bd where a, b, c and d, in that order, are four ocnsecutive natural numbers (a<b).
Which of the following statements is correct?
√P is always a prime number.
√P is always a rational number, through not necessarily prime.
√P can be rational or irretional depending on the numbers.
√P is always an irrational number.
The correct Answer is:B
To solve the problem step by step, we will evaluate the expression P=b2c2−ac−bd where a,b,c,d are four consecutive natural numbers.
Step 1: Define the consecutive natural numbers
Let’s define the four consecutive natural numbers:
- Let a=n
- Let b=n+1
- Let c=n+2
- Let d=n+3
Step 2: Substitute the values into the expression
Now we substitute a,b,c,d into the expression for P:
P=(n+1)2(n+2)2−n(n+2)−(n+1)(n+3)
Step 3: Expand the expression
Now we will expand each term:
1. Expand (n+1)2:
(n+1)2=n2+2n+1
2. Expand (n+2)2:
(n+2)2=n2+4n+4
3. Now multiply these two expansions:
(n2+2n+1)(n2+4n+4)=n4+6n3+13n2+8n+4
4. For −n(n+2):
−n(n+2)=−n2−2n
5. For −(n+1)(n+3):
−(n+1)(n+3)=−n2−4n−3
Step 4: Combine all terms
Now we combine all the terms:
P=(n4+6n3+13n2+8n+4)−(n2+2n)−(n2+4n+3)
P=n4+6n3+13n2+8n+4−n2−2n−n2−4n−3
P=n4+6n3+(13n2−2n−4n−2n)+(8n−2n−4n)+(4−3)
P=n4+6n3+11n2+2n+1
Step 5: Evaluate P for specific values of n
Let’s evaluate P for the first few values of n:
1. For n=1:
P=14+6(13)+11(12)+2(1)+1=1+6+11+2+1=21
√P=√21 (not prime)
2. For n=2:
P=24+6(23)+11(22)+2(2)+1=16+48+44+4+1=113
√P=√113 (not prime)
3. For n=3:
P=34+6(33)+11(32)+2(3)+1=81+162+99+6+1=349
√P=√349 (not prime)
Conclusion
From the evaluations, we can see that √P does not consistently yield a prime number.
Let’s define the four consecutive natural numbers:
- Let a=n
- Let b=n+1
- Let c=n+2
- Let d=n+3
Now we substitute a,b,c,d into the expression for P:
P=(n+1)2(n+2)2−n(n+2)−(n+1)(n+3)
Now we will expand each term:
1. Expand (n+1)2:
(n+1)2=n2+2n+1
2. Expand (n+2)2:
(n+2)2=n2+4n+4
3. Now multiply these two expansions:
(n2+2n+1)(n2+4n+4)=n4+6n3+13n2+8n+4
−n(n+2)=−n2−2n
−(n+1)(n+3)=−n2−4n−3
Now we combine all the terms:
P=(n4+6n3+13n2+8n+4)−(n2+2n)−(n2+4n+3)
P=n4+6n3+13n2+8n+4−n2−2n−n2−4n−3
P=n4+6n3+(13n2−2n−4n−2n)+(8n−2n−4n)+(4−3)
P=n4+6n3+11n2+2n+1
Let’s evaluate P for the first few values of n:
P=14+6(13)+11(12)+2(1)+1=1+6+11+2+1=21
√P=√21 (not prime)
P=24+6(23)+11(22)+2(2)+1=16+48+44+4+1=113
√P=√113 (not prime)
P=34+6(33)+11(32)+2(3)+1=81+162+99+6+1=349
√P=√349 (not prime)
From the evaluations, we can see that √P does not consistently yield a prime number.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - NUMBER SYSTEMEXERCISE - Test Yourself15videos
NUMBER SYSTEM
- BOOK - DISHA PUBLICATIONCHAPTER - NUMBER SYSTEMEXERCISE - Standard Level45videos
NUMBER SYSTEM
- BOOK - DISHA PUBLICATIONCHAPTER - MOCK TEST 2 EXERCISE - Multiple Choice Questions20videos
MOCK TEST 2
- BOOK - DISHA PUBLICATIONCHAPTER - PERCENTAGESEXERCISE - PRACTICE EXERCISE (TEST YOURSELF)15videos
PERCENTAGES
Similar Questions
Knowledge Check
- Question 1 - Select One or More
For the reaction
A+B→2C+D which of the following statements is/are correct?ARate of disappearance of B = 1/2 x rate of appearance of CBRate of disappearance of B =1/2 x rate of appearance of CCRate of disappearance of A = rate of appearance of BDRate of disapperance of A = rate of disapperance of B. - Question 2 - Select One
For the reaction of 4A+B→2C+D.. Which of the following statements is correct ?
AThe rate of formation of C and D are equalBThe rate of formation of D is one half the rate of consumption of ACThe rate of appearance of C is one half the rate of disappearance of BDThe rate of disappearance of B is one fourth of the rate of disappearance of A - Question 3 - Select One
Consider the following structures (A),(B),(C) and (D).

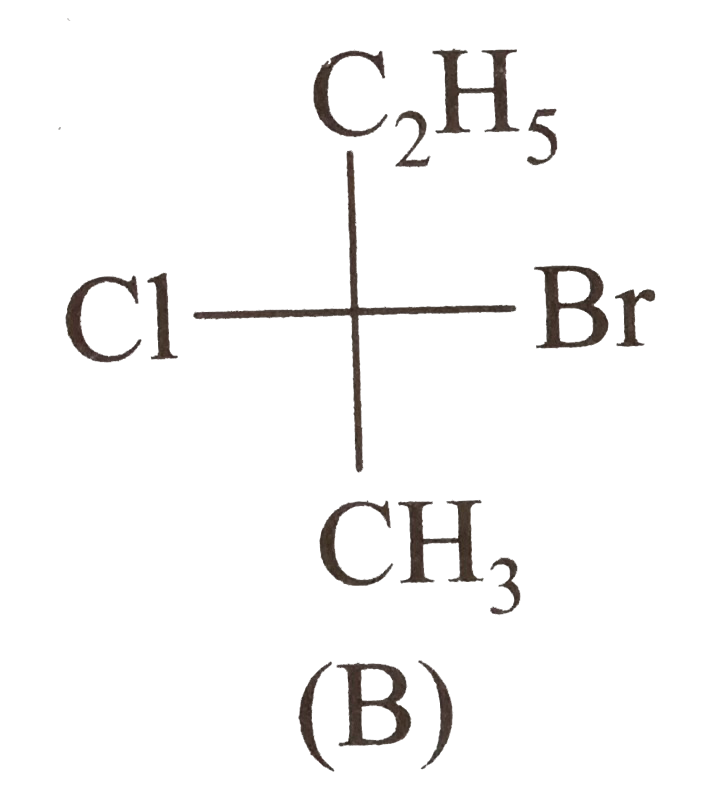

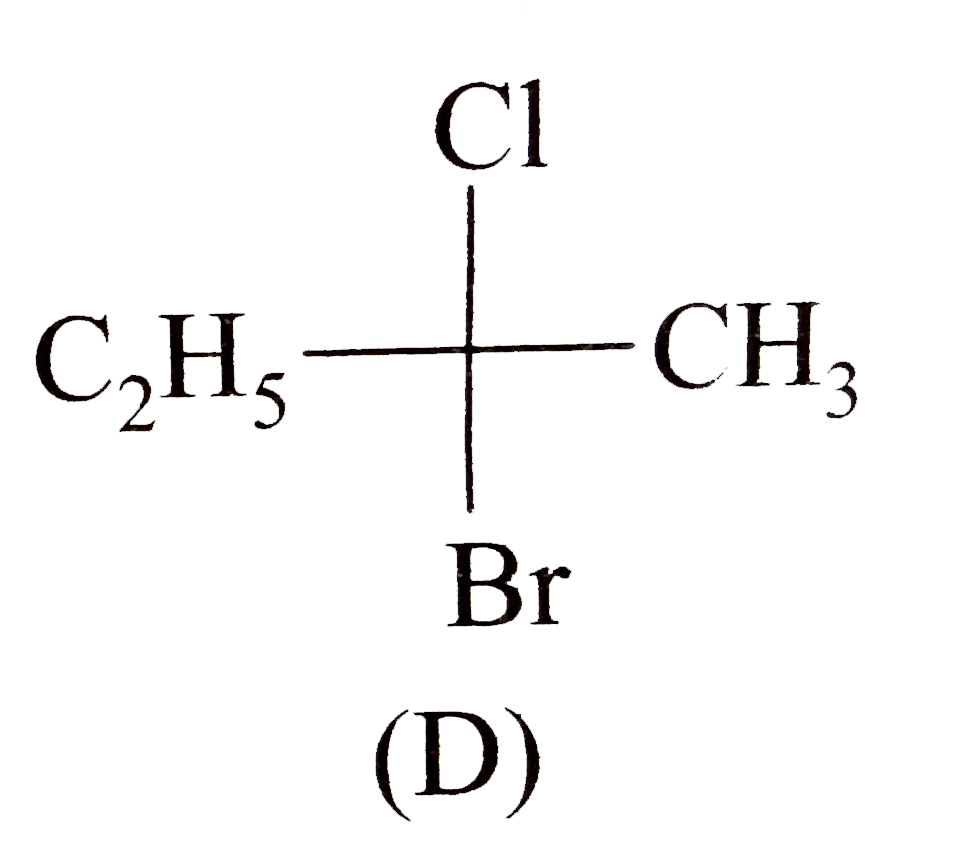
Which of the following statements is not correct?A(A)and(C) are enantiomersB(A)and(B)are enantiomersC(B)and(D)are enantiomersD(B)and(C)are identical
Consider the following statements about natural numbers: There exists a smallest natural number. There exists a largest natural number. Between two natural numbers, there is always a natural number. Which of the above statements is/are correct? None (b) Only1 (c) 1 and 2 (d) 2 and 3
View SolutionNumber of ordered triplets of natural number (a,b,c) for which abc≤11 is
View SolutionThe median BD of the triangle ABC meets AC at D. If BD=12AC , then which one of the following is correct ?
View SolutionConsider the following configurations (A),(B),(C) and (D)
(A)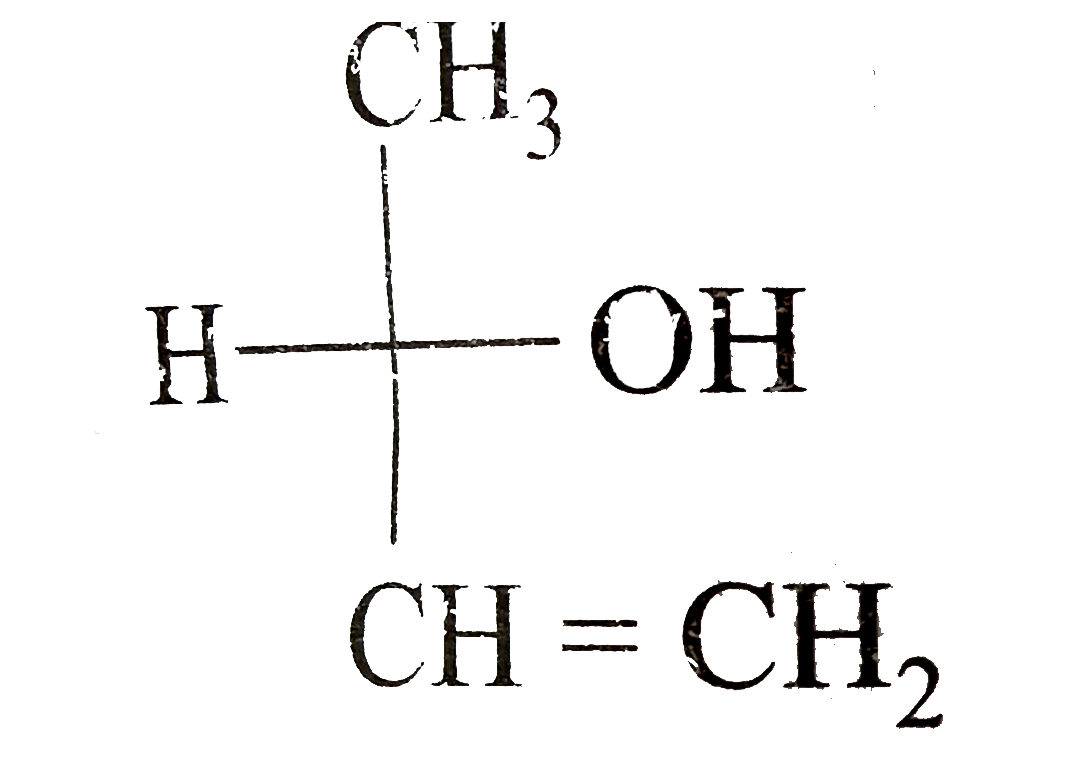
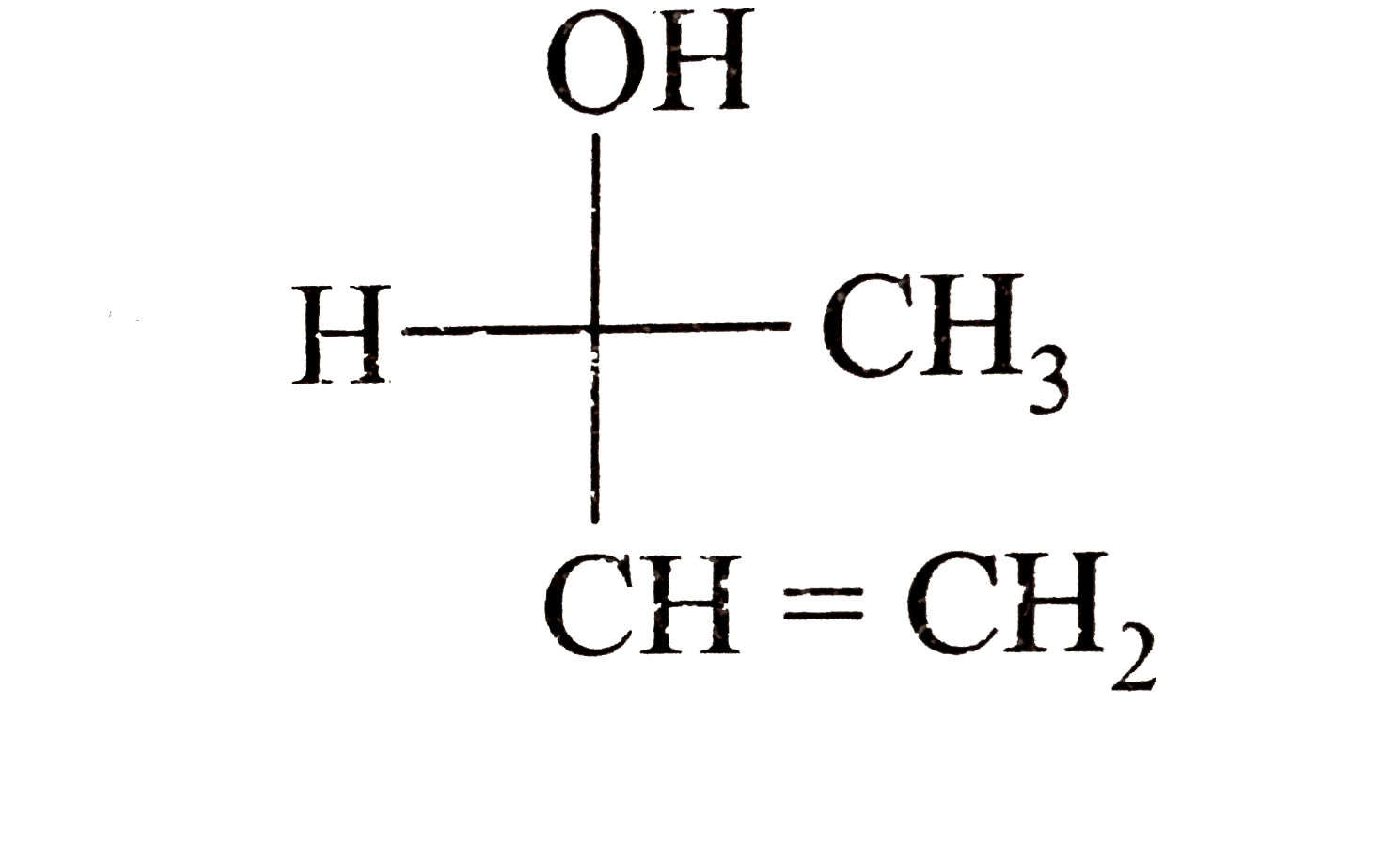
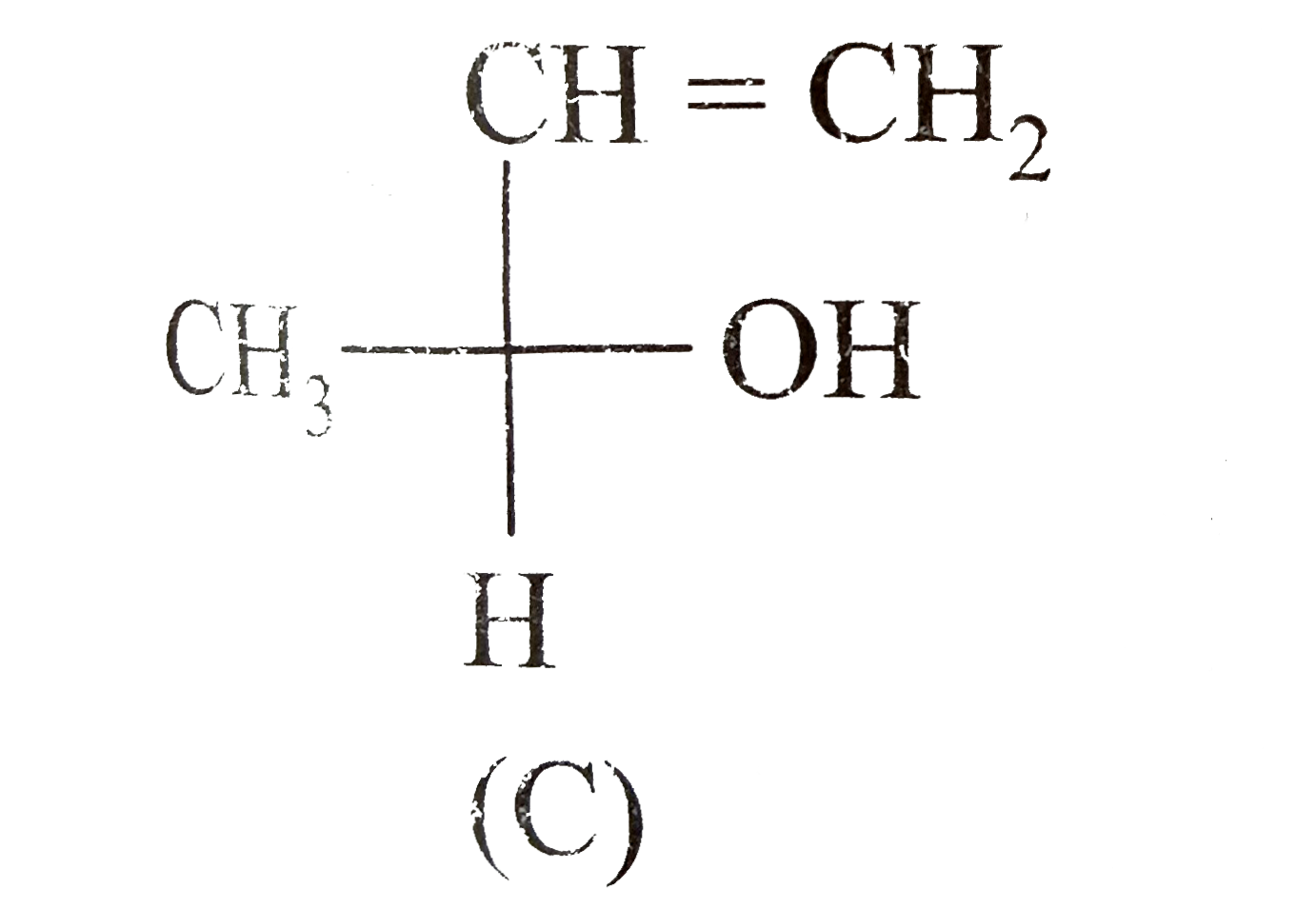
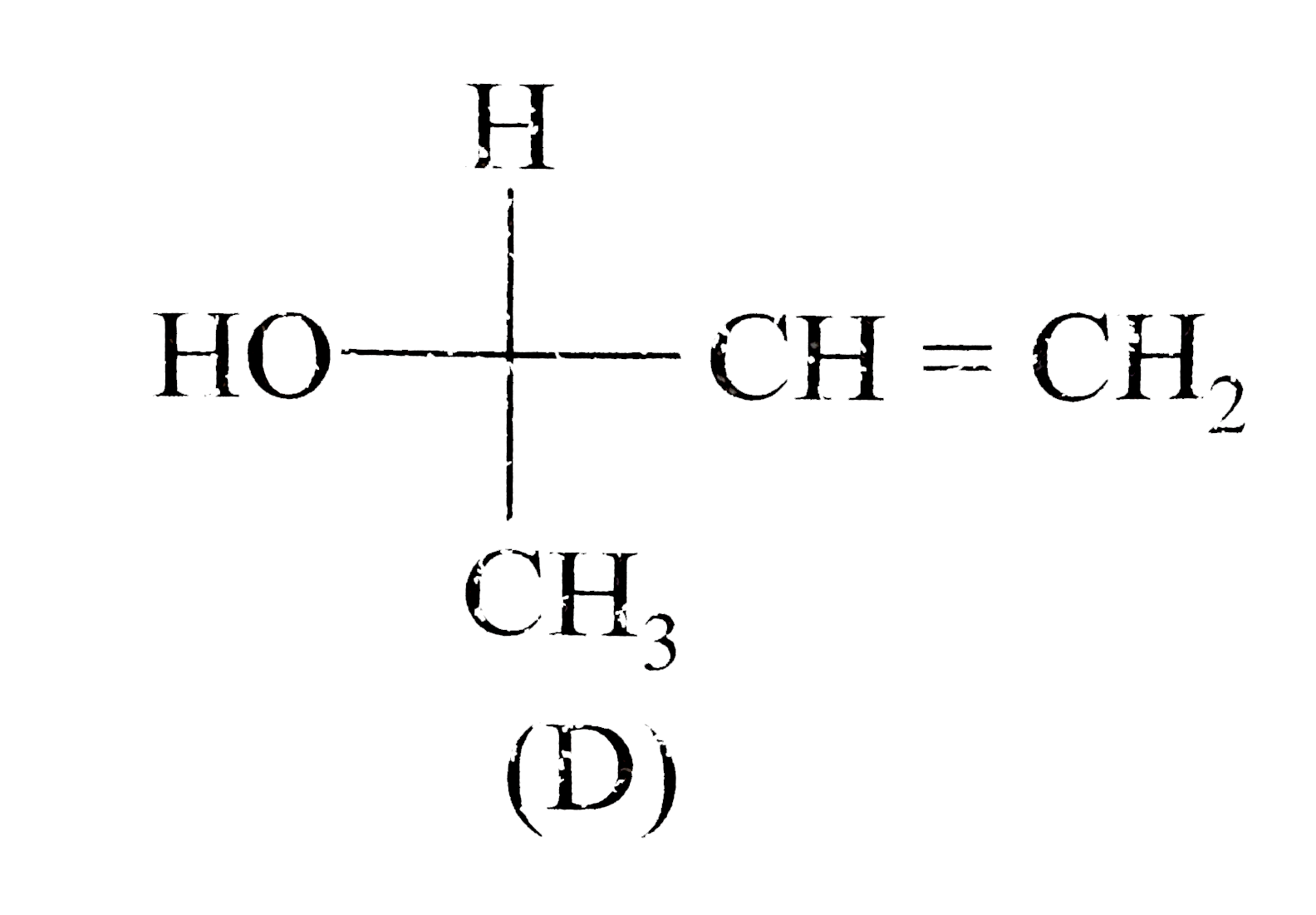
which of the following statements is not correct?View SolutionIf a,b,c and d are four unequal positive numbers which are in A.P then
View Solution

