N=70!×69!×68!×….3!×2!×1!
Which of the following represents the 147th digit from the right end of N?
2
0
5
7
The correct Answer is:B
To solve the problem of finding the 147th digit from the right end of the number N=70!×69!×68!×…×3!×2!×1!, we need to determine how many trailing zeros are present in N.
1. Understanding Trailing Zeros:
Trailing zeros in a factorial are produced by the factors of 10 in the number, which are formed by pairs of 2 and 5. Since there are generally more factors of 2 than 5, the number of trailing zeros is determined by the number of times 5 is a factor in the factorial.
2. Calculating Trailing Zeros for Each Factorial:
We need to calculate the number of trailing zeros contributed by each factorial from 1! to 70!.
The formula to find the number of trailing zeros in n! is:
Trailing Zeros(n!)=⌊n5⌋+⌊n25⌋+⌊n125⌋+…
3. Calculating Trailing Zeros for Each Factorial:
- For 1! to 4!:
Trailing Zeros=0
- For 5! to 9!:
Trailing Zeros=1(from 5!)
- For 10! to 14!:
Trailing Zeros=2(from 10!)
- For 15! to 19!:
Trailing Zeros=3(from 15!)
- Continuing this way, we can calculate the trailing zeros for all factorials up to 70!.
4. Summing Up the Trailing Zeros:
By calculating the trailing zeros for each factorial up to 70!, we find:
- 70!: 14 zeros
- 69!: 13 zeros
- 68!: 13 zeros
- ...
- 5!: 1 zero
- 4!: 0 zeros
- 3!: 0 zeros
- 2!: 0 zeros
- 1!: 0 zeros
When we sum all these zeros, we find that there are a total of 155 trailing zeros in N.
5. Finding the 147th Digit from the Right:
Since there are 155 trailing zeros in N, the 147th digit from the right end of N must also be a zero.
Conclusion:
The 147th digit from the right end of N is 0.
Trailing zeros in a factorial are produced by the factors of 10 in the number, which are formed by pairs of 2 and 5. Since there are generally more factors of 2 than 5, the number of trailing zeros is determined by the number of times 5 is a factor in the factorial.
We need to calculate the number of trailing zeros contributed by each factorial from 1! to 70!.
Trailing Zeros(n!)=⌊n5⌋+⌊n25⌋+⌊n125⌋+…
- For 1! to 4!:
Trailing Zeros=0
- For 5! to 9!:
Trailing Zeros=1(from 5!)
- For 10! to 14!:
Trailing Zeros=2(from 10!)
- For 15! to 19!:
Trailing Zeros=3(from 15!)
- Continuing this way, we can calculate the trailing zeros for all factorials up to 70!.
By calculating the trailing zeros for each factorial up to 70!, we find:
- 70!: 14 zeros
- 69!: 13 zeros
- 68!: 13 zeros
- ...
- 5!: 1 zero
- 4!: 0 zeros
- 3!: 0 zeros
- 2!: 0 zeros
- 1!: 0 zeros
Since there are 155 trailing zeros in N, the 147th digit from the right end of N must also be a zero.
The 147th digit from the right end of N is 0.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - NUMBER SYSTEMEXERCISE - Test Yourself15videos
NUMBER SYSTEM
- BOOK - DISHA PUBLICATIONCHAPTER - NUMBER SYSTEMEXERCISE - Standard Level45videos
NUMBER SYSTEM
- BOOK - DISHA PUBLICATIONCHAPTER - MOCK TEST 2 EXERCISE - Multiple Choice Questions20videos
MOCK TEST 2
- BOOK - DISHA PUBLICATIONCHAPTER - PERCENTAGESEXERCISE - PRACTICE EXERCISE (TEST YOURSELF)15videos
PERCENTAGES
Similar Questions
Knowledge Check
- Question 1 - Select One
If the product of 1×2×3×4×…n contains 68 zeros in the end of the number. Then the maximum possible number of values of n is:
A1B3C5D6 - Question 2 - Select One
If 1×2×3×…….×n is denoted by
 , then
, then 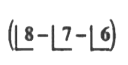 is equal to : A
is equal to : A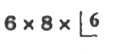 B
B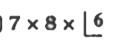 C
C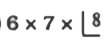 D
D
- Question 3 - Select One
Let P(n):2n<(1×2×3×….×n) . Then the smallest positive integers for which P(n ) is true , is
A1B2C3D4
In an A.P. if m times the mth term is equal to n times the nth term then find (m+n)th term.
View SolutionWhat is the unit digit of 368×473×15101?
View SolutionLet P(n):2n<(1×2×3××n) . Then the smallest positive integer for which P (n) is true is
View SolutionIf the unit digit of (433×456×43N) is (N+2), then what is the value of N ?
View SolutionSolve the followings :
(am−n)1×(an−1)m×(a1−m)nView Solution

