In a group of 50 people, two tests were conducted, one for diabetes and one for blood pressure. 30 people were diagnosed with diabetes and 40 people were diagnosed with high blood pressure. What is the minimum number of people who were having diabetes and high blood pressure?
0
10
20
30
The correct Answer is:C
To solve the problem, we need to find the minimum number of people who have both diabetes and high blood pressure. We can use the principle of inclusion-exclusion in set theory.
1. Define the Sets:
- Let A be the set of people diagnosed with diabetes.
- Let B be the set of people diagnosed with high blood pressure.
2. Identify the Sizes of the Sets:
- The number of people in set A (diabetes) is |A|=30.
- The number of people in set B (high blood pressure) is |B|=40.
3. Total Number of People:
- The total number of people in the group is |A∪B|=50.
4. Use the Inclusion-Exclusion Principle:
- According to the principle, the total number of people in either set A or set B can be expressed as:
|A∪B|=|A|+|B|−|A∩B|
- Where |A∩B| is the number of people who have both conditions (diabetes and high blood pressure).
5. Substitute the Known Values:
- We know:
50=30+40−|A∩B|
6. Simplify the Equation:
- Rearranging the equation gives:
50=70−|A∩B|
- Therefore:
|A∩B|=70−50=20
7. Conclusion:
- The minimum number of people who have both diabetes and high blood pressure is |A∩B|=20.
Final Answer:
The minimum number of people who were having both diabetes and high blood pressure is 20.
- Let A be the set of people diagnosed with diabetes.
- Let B be the set of people diagnosed with high blood pressure.
- The number of people in set A (diabetes) is |A|=30.
- The number of people in set B (high blood pressure) is |B|=40.
- The total number of people in the group is |A∪B|=50.
- According to the principle, the total number of people in either set A or set B can be expressed as:
|A∪B|=|A|+|B|−|A∩B|
- Where |A∩B| is the number of people who have both conditions (diabetes and high blood pressure).
- We know:
50=30+40−|A∩B|
- Rearranging the equation gives:
50=70−|A∩B|
- Therefore:
|A∩B|=70−50=20
- The minimum number of people who have both diabetes and high blood pressure is |A∩B|=20.
The minimum number of people who were having both diabetes and high blood pressure is 20.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a group of 50 people, two sets were conducted, one for diabetes and one for blood pressure. 30 people were diagnosed with diabetes and 40 people were diagnosed with high blood pressure. What is the minimum number of people who were having diabetes and high blood pressure ?
A0B10C20D30Assertion : Generally old people have hiher blood pressure.
Reason : Arterial diameter increases with Age.AIf both Assertion & Reason are True & the Reason is a correct explanation of the Assertion .BIf both Assertion & Reason are True but Reason is not a correct explanation of the AssertionCIf Assertion is True but the Reason is False.DIf both Assertion & Reason are false.A marketing company conducted a survey among 10,000 person in Kanpur :
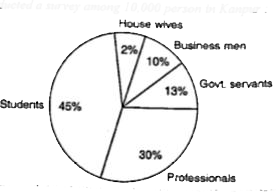
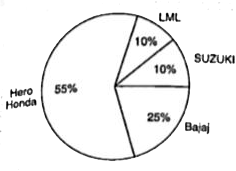
It was observed that some people have more than one bike but from only one company i.e., a particular person can have more than one bike of HeroHonda, but not from bajaj etc. and vice versa. Thus there were total 12,000 bikes with 10,000 persons used for survey. There are only four compaies operating in this market.
If the number of people who drive one, two and three bikes are in the ratio 15 : 3 : 1 what is the number of people in the survey who do not drive even a single bike ?A750B400C600D500
Study the following information carefully and answer the given questions:
The diagram, given below shows the data related to loan fair. In total z number of people contacted for a loan fair, from which x number of people visited loan fair and 9600 people shown interest for a loan. Out of the total number of people shown interest for a loan only 32% applied for the loan. Out of the total number of people applied for the loan, only 20% are eligible for a loan. Out of the total number of people eligible for a loan, loan of only y% people are disbursed

Loan of 40% of the people did not disbursed who were eligible for a loan, then find the ratio of the number of people, who shown interest and the number of people, whose loan disbursed.
View SolutionCertain number of people work in three farms. A , B and C . Three are only type farms and each person works in one or more farms. 72% of people were in farm and people working in only farms C was 136the of people working in farm A. Number of people working in both B and C but not in Farm A are 55. people working in only farms B are 65 more thn the people working in only farm C.
Number of people working in only farm A is 1603% more than number of people working in farm B.
What is the number of people who working in farm, A but not only in farm ?
View SolutionCertain number of people work in three farms. A , B and C . Three are only type farms and each person works in one or more farms. 72% of people were in farm and people working in only farms C was 136the of people working in farm A. Number of people working in both B and C but not in Farm A are 55. people working in only farms B are 65 more thn the people working in only farm C.
Number of people working in only farm A is 1603% more than number of people working in farm B.
What is the number of people working in farm B only ?
View SolutionA man bought an article and sold it at a gain of 5 %. If he had bought it at 5% less and sold it for Re 1 less, he would have made a profit of 10%. The C.P. of the article was
View SolutionThe cash difference between the selling prices of an article at a profit of 4% and 6% is Rs 3. The ratio of two selling prices is
View Solution
