Which one of the following is an example of nonempty set?
Set of all even prime numbers
{x:x2−2=0andx is rational}
{x: x is a natural number, x<8 and simultaneously x>12)
{X: is a point common to any two parallel lines}
The correct Answer is:A
To determine which of the given options is an example of a non-empty set, we need to analyze each option carefully. A non-empty set is defined as a set that contains at least one element. Let's go through the options step by step.
1. Evaluate the first option: Set of all even prime numbers.
- The only even prime number is 2.
- Therefore, this set contains one element: {2}.
- Since it contains an element, this is a non-empty set.
2. Evaluate the second option: x is a rational number such that x² - 2 = 0.
- To solve for x, we rearrange the equation: x² = 2.
- Taking the square root gives us x = ±√2.
- However, √2 is not a rational number; it is an irrational number.
- Therefore, there are no rational numbers that satisfy this equation, making this set empty.
3. Evaluate the third option: x is a natural number, x < 8 and x > 12.
- The condition x < 8 gives us the natural numbers {1, 2, 3, 4, 5, 6, 7}.
- The condition x > 12 gives us the natural numbers {13, 14, 15, ...}.
- There are no natural numbers that can satisfy both conditions simultaneously, resulting in an empty set.
4. Evaluate the fourth option: x is a point common to any two parallel lines.
- By definition, parallel lines do not intersect; hence, there cannot be a common point.
- This means there are no elements in this set, making it empty.
Conclusion:
Based on the evaluations:
- The first option (Set of all even prime numbers) is a non-empty set.
- The second, third, and fourth options are empty sets.
Thus, the answer is that the first option is an example of a non-empty set.
- The only even prime number is 2.
- Therefore, this set contains one element: {2}.
- Since it contains an element, this is a non-empty set.
- To solve for x, we rearrange the equation: x² = 2.
- Taking the square root gives us x = ±√2.
- However, √2 is not a rational number; it is an irrational number.
- Therefore, there are no rational numbers that satisfy this equation, making this set empty.
- The condition x < 8 gives us the natural numbers {1, 2, 3, 4, 5, 6, 7}.
- The condition x > 12 gives us the natural numbers {13, 14, 15, ...}.
- There are no natural numbers that can satisfy both conditions simultaneously, resulting in an empty set.
- By definition, parallel lines do not intersect; hence, there cannot be a common point.
- This means there are no elements in this set, making it empty.
Based on the evaluations:
- The first option (Set of all even prime numbers) is a non-empty set.
- The second, third, and fourth options are empty sets.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Which one of the following is an example of non-empty set ?
ASet of all even prime numbersB(x:x2−2=0 and x is rational)C{x:x is a natural number, x<8 and simultaneously x>12}D{x:x is a point common to any two parallel lines} - Question 2 - Select One
Which one of the following is an example of a thermosetting polymer?
A⎛⎜⎝−CH3−C∣Cl=CH−CH2−⎞⎟⎠nB⎛⎜⎝−CH2−CH∣Cl−⎞⎟⎠nC⎛⎜⎝−H∣N−(CH3)6−H∣N−O∣∣C−(CH3)4−O∣∣C−⎞⎟⎠nD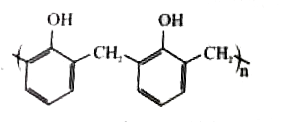
- Question 3 - Select One
Which one of the following is an example of reinforcement ?
ANo Lata, the answer is not 45BKamla, can't your help Keerti with her anserCOh no as usual, you are wrongDSuniti , you have said rightly
Which one of the following is an example of platyhelminthes
View SolutionWhich one of the following is an example of cleistogamy ?
View SolutionWhich one of the following is an example of donor impurity?
View SolutionWhich one of the following is an example of systematic error?
View SolutionWhich one of the following is an example of cleistogamy or Even in absence of pollinating agents seed setting is assured in
View Solution

