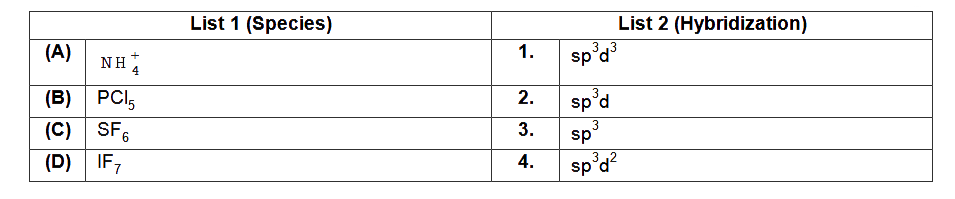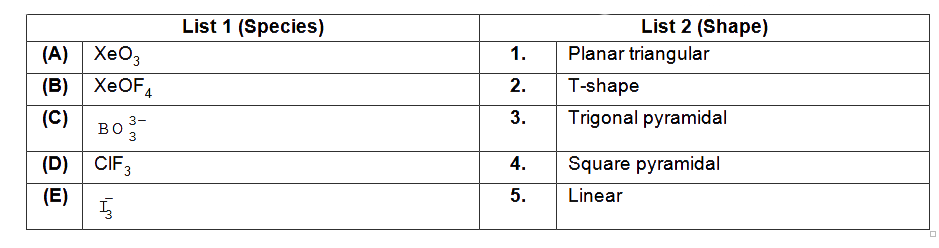For a square matrix A. which of the following properties hold ?
I. (A−1)−1=A
II. Det (A−1)=1detA
III. (λA)−1 where λ is a scalar Select the correct answer using the code given below :
I and II only
II and III only
I and III only
1,2 and 3 only
To solve the question regarding the properties of a square matrix A, we will analyze each of the given statements one by one.
Step 1: Analyze Property I
Statement: (A−1)−1=A
Solution:
The inverse of a matrix A, denoted as A−1, is defined such that when multiplied by A, it yields the identity matrix I:
A⋅A−1=I
Now, if we take the inverse of A−1, we are looking for a matrix that, when multiplied by A−1, gives us I. By the definition of the inverse, we have:
(A−1)−1=A
Thus, this property is true.
Step 2: Analyze Property II
Statement: Det(A−1)=1Det(A)
Solution:
The determinant of the inverse of a matrix has a specific relationship with the determinant of the original matrix. The property states:
Det(A−1)=1Det(A)
This is a well-known property of determinants. Therefore, this property is also true.
Step 3: Analyze Property III
Statement: (λA)−1 where λ is a scalar
Solution:
The inverse of a scalar multiplied by a matrix can be expressed as:
(λA)−1=1λA−1
This means that the inverse of λA is not simply A−1, but rather it includes the factor 1λ. Therefore, this property is false.
Conclusion
From the analysis above, we conclude:
- Property I is true.
- Property II is true.
- Property III is false.
Thus, the correct answer is that only Properties I and II are true.
Final Answer
The correct answer is: I and II only.
---
Statement: (A−1)−1=A
The inverse of a matrix A, denoted as A−1, is defined such that when multiplied by A, it yields the identity matrix I:
A⋅A−1=I
Now, if we take the inverse of A−1, we are looking for a matrix that, when multiplied by A−1, gives us I. By the definition of the inverse, we have:
(A−1)−1=A
Thus, this property is true.
Statement: Det(A−1)=1Det(A)
The determinant of the inverse of a matrix has a specific relationship with the determinant of the original matrix. The property states:
Det(A−1)=1Det(A)
This is a well-known property of determinants. Therefore, this property is also true.
Statement: (λA)−1 where λ is a scalar
The inverse of a scalar multiplied by a matrix can be expressed as:
(λA)−1=1λA−1
This means that the inverse of λA is not simply A−1, but rather it includes the factor 1λ. Therefore, this property is false.
From the analysis above, we conclude:
- Property I is true.
- Property II is true.
- Property III is false.
The correct answer is: I and II only.
Topper's Solved these Questions
Similar Questions
Knowledge Check
For a square matrix A, which of the following properties hold ?
1. (A−1)−1=A
2. det(A−1)=1detA
3. (λA)−1λA−1 where λ is a scalar
Select the correct answer using the code given below :A1 and 2 onlyB2 and 3 onlyC1 and 3 onlyD1, 2 and 3Match 1list I with list II and select the correct answer using the code given below
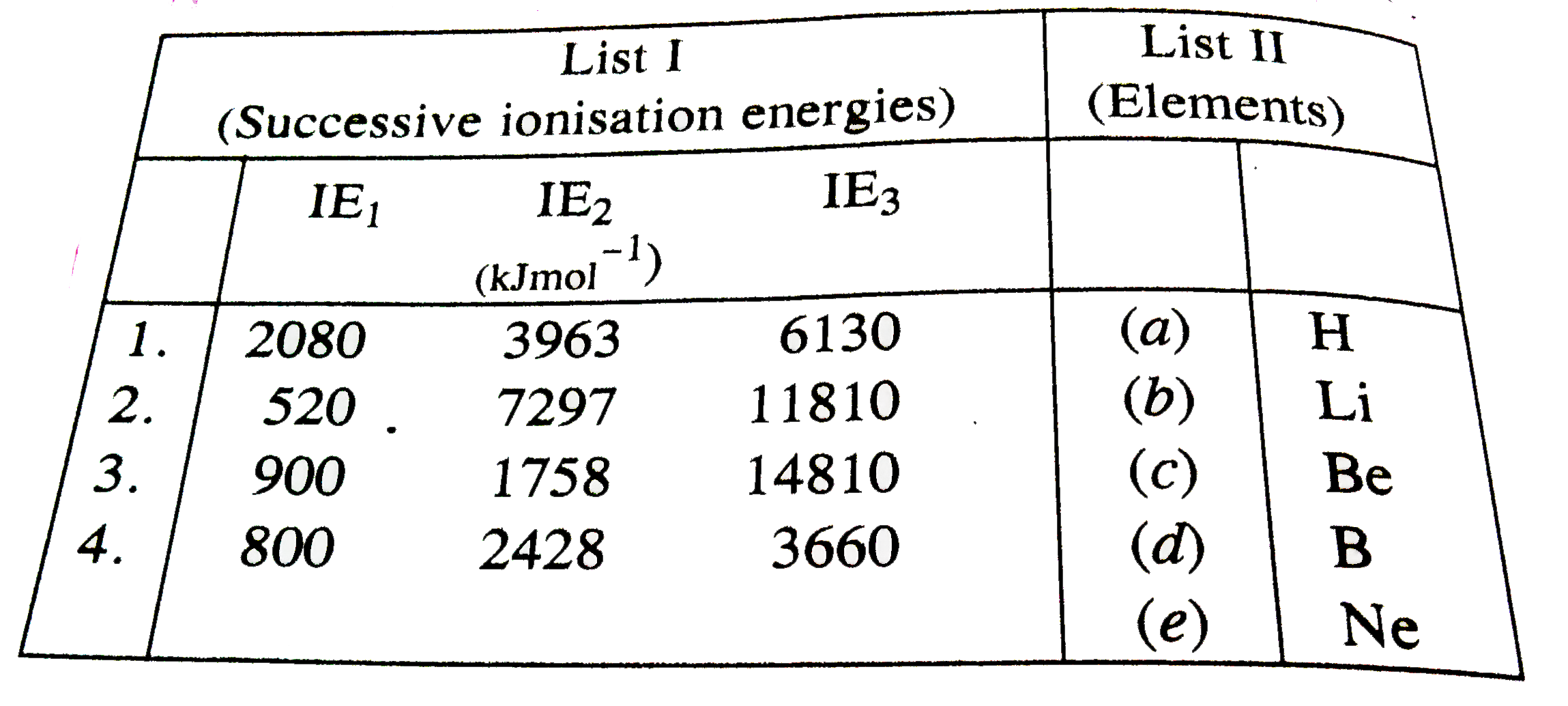 A1.c,2. b,3.d ,4.eB1. a,2. c, 3. b, 4.dC1. d, 2. a, 3. b , 4. dD1. e,2. b,3. c,4. d
A1.c,2. b,3.d ,4.eB1. a,2. c, 3. b, 4.dC1. d, 2. a, 3. b , 4. dD1. e,2. b,3. c,4. dMatch list - 1 with ist -- Il and select the correct answer using the codes given below.
 A3412B3142C3421D4321
A3412B3142C3421D4321
Match List 1 with List 2. Select the correct answer using the codes given below the list.
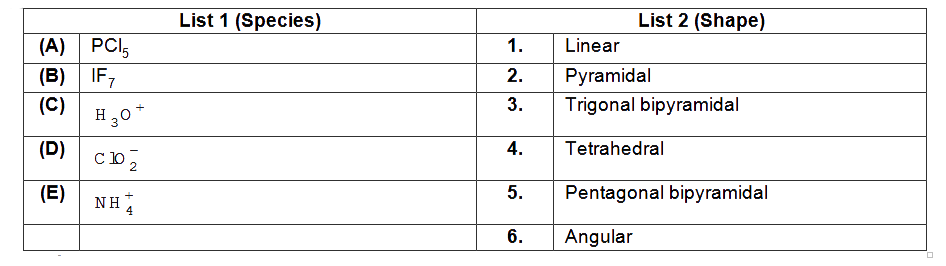
View SolutionMatch List I with List II and select the correct answer using the codes given below :

Codes
View SolutionMatch list - 1 with ist -- Il and select the correct answer using the codes given below.

View SolutionMatch Column I with Column II and select the correct answer using the codes given below :

Answer codes:
View SolutionMatch Column I with Column II and select the correct answer using the codes given below :

Answer codes:
View Solution