The matrix A has x rows and x+5 columns The matrix B has y rows and 11-y columns both AB and BA exist. What are the values of the x and y respectively ?
8 and 3
3 and 4
3 and 8
8 and 8
To solve the problem, we need to find the values of x and y such that both the products AB and BA exist.
1. Understanding Matrix Dimensions:
- Matrix A has x rows and x+5 columns.
- Matrix B has y rows and 11−y columns.
2. Condition for Matrix Multiplication AB:
- For the product AB to exist, the number of columns in A must equal the number of rows in B.
- Thus, we have:
x+5=y(Equation 1)
3. Condition for Matrix Multiplication BA:
- For the product BA to exist, the number of columns in B must equal the number of rows in A.
- Thus, we have:
11−y=x(Equation 2)
4. Substituting Equation 1 into Equation 2:
- From Equation 1, we can express y in terms of x:
y=x+5
- Now substitute y into Equation 2:
11−(x+5)=x
- Simplifying this gives:
11−x−5=x
6−x=x
6=2x
x=3
5. Finding y:
- Now substitute x=3 back into Equation 1:
y=3+5=8
6. Final Values:
- The values of x and y are:
x=3,y=8
Conclusion:
The values of x and y respectively are 3 and 8.
- Matrix A has x rows and x+5 columns.
- Matrix B has y rows and 11−y columns.
- For the product AB to exist, the number of columns in A must equal the number of rows in B.
- Thus, we have:
x+5=y(Equation 1)
- For the product BA to exist, the number of columns in B must equal the number of rows in A.
- Thus, we have:
11−y=x(Equation 2)
- From Equation 1, we can express y in terms of x:
y=x+5
- Now substitute y into Equation 2:
11−(x+5)=x
- Simplifying this gives:
11−x−5=x
6−x=x
6=2x
x=3
- Now substitute x=3 back into Equation 1:
y=3+5=8
- The values of x and y are:
x=3,y=8
The values of x and y respectively are 3 and 8.
Topper's Solved these Questions
Similar Questions
The matrix A has x rows and (x+5) column. If the matrix B has y rows and (11−y) columns & both ABandBA exist, then x=8 (b) x=3 y=6 (d) y=8
View SolutionMatrix A has (2y+1) rows and (x+9) columns matrix B has (19-x) rows and (y+3) columns.If both AB and BA exist then the value of (x+2y) is equal to
View Solution
Knowledge Check
Matrix A has x rows and x+5 columns. Matrix B has y rows and 11−y columns. If both AB and BA exist, then the ordered pair (x, y) is
A(3, 3)B(8, 3)C(3, 8)Dnone of theseIf a matrix X has (a+b) rows and (a+2) columns and a matrix Y has (b+1) rows and (a+3) columns If both XY and YX exist. Then what are the values of a,b respectively ?
A3,2B2,3C2,4D4,3If sum of each row, column and diagonals are equal, then the value of x, y, z and w respectively, is
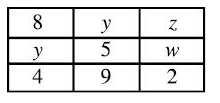 A4, 6, 8, 7B1, 3, 6, 7C1, 6, 3,7D3, 6, 7, 1
A4, 6, 8, 7B1, 3, 6, 7C1, 6, 3,7D3, 6, 7, 1
Matrix A has x rows and x+4 columns and another matrix B has y rows and 2y−10 columns Both AB and BA exist then x+y
View SolutionMatrix A ha s m rows and n+ 5 columns; matrix B has m rows and 11−n columns. If both AB and BA exist, then (A) AB and BA are square matrix (B) AB and BA are of order 8×8 and 3×13, respectively (C) AB=BA (D) None of these
View SolutionA matrix X has a+b rows and a+2 columns while the matrix Y has b+1 rows and a+3 columns. Both matrices XY and YX exist. Find a and b . Can you say XY and YX are of the same type? Are they equal.
View SolutionIs it possible to define the matrix A + B when
a. A has 3 rows and B has 2 rows……………
b. A has 2 columns and B has 4 columns……………….
c. A has 3 rows and B has 2 columns…………….
d Both A and B are square matrices of the same order …………..
View SolutionIf a matrix contain 5 rows and 3 columns, then the number of elements of the matrix is _____
View Solution
