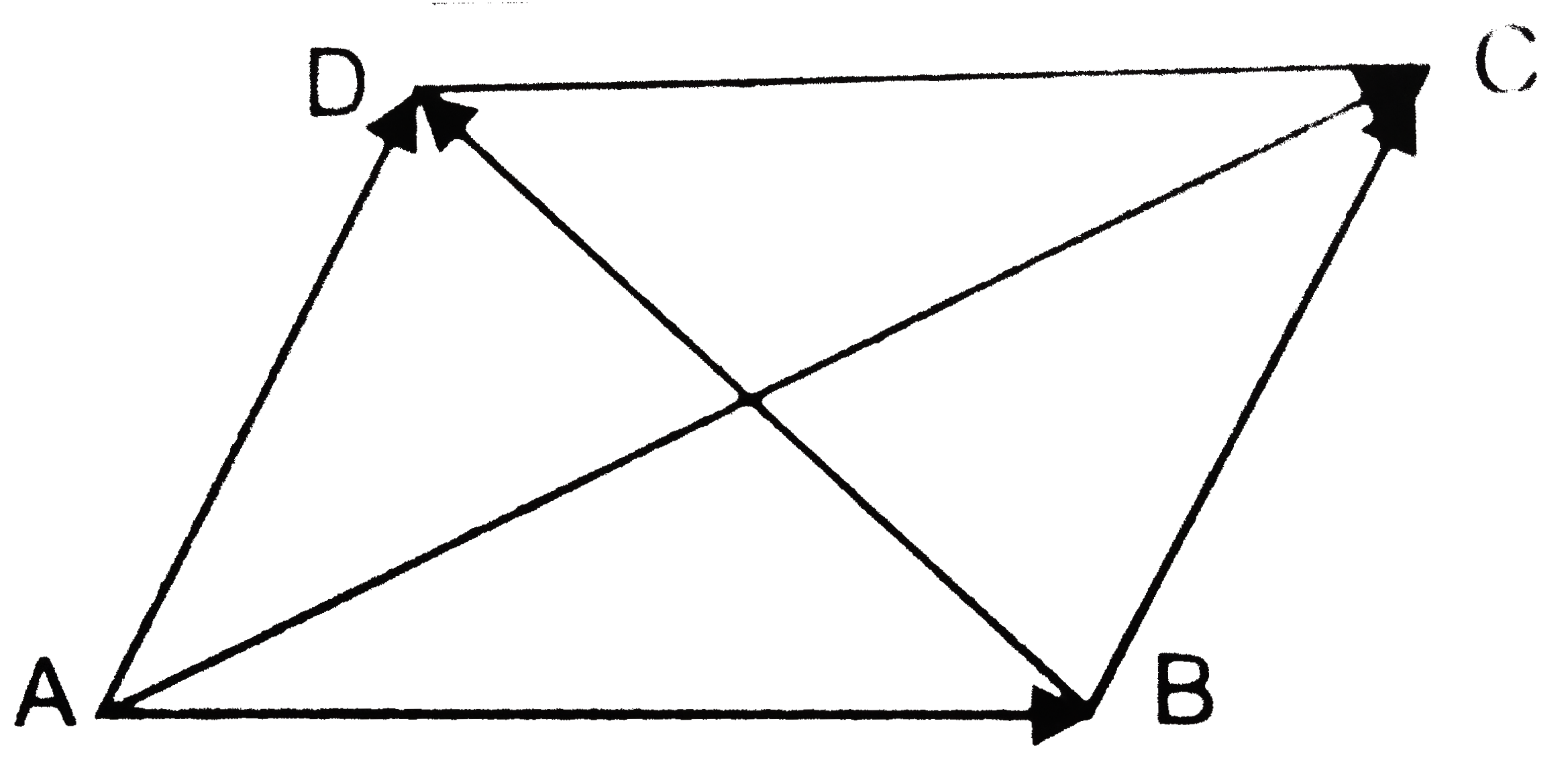
Let ABCD be a parallelogram whose diagonals intersect at P and let O be the origin. What is equal to
The correct Answer is:B
To solve the problem, we need to find the sum of the vectors from the origin O to the vertices A, B, C, and D of the parallelogram ABCD.
1. Understanding the Position Vectors:
- Let →OA, →OB, →OC, and →OD be the position vectors of points A, B, C, and D respectively from the origin O.
2. Using the Property of Midpoints:
- The diagonals of a parallelogram bisect each other. Therefore, the point P, where the diagonals AC and BD intersect, is the midpoint of both diagonals.
- For diagonal AC, we can express this as:
→OP=→OA+→OC2
- Rearranging this gives:
→OA+→OC=2→OP(Equation 1)
3. Applying the Same Concept to the Other Diagonal:
- For diagonal BD, we have:
→OP=→OB+→OD2
- Rearranging this gives:
→OB+→OD=2→OP(Equation 2)
4. Adding the Two Equations:
- Now, we add Equation 1 and Equation 2:
(→OA+→OC)+(→OB+→OD)=2→OP+2→OP
- This simplifies to:
→OA+→OB+→OC+→OD=4→OP
5. Conclusion:
- Therefore, the sum of the vectors from the origin O to the vertices A, B, C, and D is:
→OA+→OB+→OC+→OD=4→OP
Final Answer:
→OA+→OB+→OC+→OD=4→OP
- Let →OA, →OB, →OC, and →OD be the position vectors of points A, B, C, and D respectively from the origin O.
- The diagonals of a parallelogram bisect each other. Therefore, the point P, where the diagonals AC and BD intersect, is the midpoint of both diagonals.
- For diagonal AC, we can express this as:
→OP=→OA+→OC2
- Rearranging this gives:
→OA+→OC=2→OP(Equation 1)
- For diagonal BD, we have:
→OP=→OB+→OD2
- Rearranging this gives:
→OB+→OD=2→OP(Equation 2)
- Now, we add Equation 1 and Equation 2:
(→OA+→OC)+(→OB+→OD)=2→OP+2→OP
- This simplifies to:
→OA+→OB+→OC+→OD=4→OP
- Therefore, the sum of the vectors from the origin O to the vertices A, B, C, and D is:
→OA+→OB+→OC+→OD=4→OP
→OA+→OB+→OC+→OD=4→OP
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Let ABCD be a parallelogram whose diagonals intersect at P and O be the origin, then OA+OB+OC+OD equals
AOPB2OPC3OPD4OP - Question 2 - Select One
ABCD is a parallelogram with AC and BD as diagonals. Then, A→C−B→D=
A4A→BB3A→BC2A→BDA→B - Question 3 - Select One
If ABCD is a parallelogram, then −−→AC−−−→BD=
A4−−→ABB3−−→ABC2−−→ABD−−→AB
If ABCD is a rhombus whose diagonals cut at the origin O, then proved that →OA+→OB+→OC+→OD+→O.
View SolutionABCD is a parallelogram Fig. 2 (c ) .64. ACand(BD)areitsdiagonals.Showtˆ<br> (a) vec (AC) +vec (BD) =2 vec (BC)<br>(b)vec (AC) - vec (BD) =2 vec (AB)
 . View Solution
. View SolutionABCD is parallelogram and P is the point of intersection of its diagonals. If O is the origin of reference, show that →OA+→OB+→OC+→OD=4→OP.
View SolutionIf ABCD is a rombus whose diagonals cut at the origin O, then OA + OB + OC + OD equals to
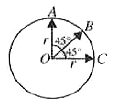
View SolutionThe resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure is
 View Solution
View Solution

