Show that the motion of a simple pendulum is simple harmonic. Hence find an expression for its time period.

Text Solution

Verified by Experts

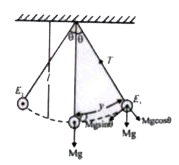
Let the bob of simple pendulum be oscillating between two extreme positions $E_{1}$ and $E_{2}$ . If bob is displaced from mean position O, to extreme point $E_{1}$ , then various force acting on the bob at point $E_{1}$ are as follows :
(i) Weing of the bob, $W = M g$
(ii) Tention in the string , T
The weightMg can be resolved into two components :
(a) $M g \sin θ = F$ , restoring force.
But F=Ma (Newton.s second law)
$\Rightarrow Ma = - M g \sin θ$
Here the $- v e$ sigh shows the restoring nature of the force
$\Rightarrow a = - g \sin θ$
since $θ$ is very-very small, so $\sin θ ≅ θ$ , therefore $a = - g θ$
or $a = \frac{- gy}{l}$ . . .. (i) $(∵ From fig . θ = \frac{y}{l})$
or $a \propto - y (∵ \frac{g}{l} = constant)$
Hence, the motion of simple pendulum is SHM.
Thus, time period of simple pendulum is given by :
$T = 2 π \sqrt{\frac{Displecement}{|Acceleration|}} or T = 2 π \sqrt{\frac{l}{g}} [Using equation (i)]$
Frequency, $v = \frac{1}{T} = \frac{1}{2 π} \sqrt{\frac{g}{l}}$ .
From above equation, its is clear that time period of simpla pendulum is independent of its mass.

Updated on:21/07/2023