Deduce Coulomb's law from Gauss's theorem in electrostatics.

Text Solution

Verified by Experts

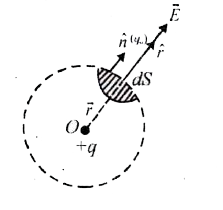
consider a point charge + at O. Imagine a sphere of radius r and with centre O. The angle between $\to E$ and $\to d S$ is zero (0°). According to Gauss.s law,
$Φ_{E} = \oint \to E . - \to d S = \frac{q}{ɛ_{0}} \Rightarrow \oint E d S {cos 0}^{\circ} = \frac{q}{ɛ_{0}}$
$\Rightarrow \oint E . d S = \frac{q}{ɛ_{0}}$
But $\oint d S = 4 π r^{2}$
$\Rightarrow E .4 π r^{2} = \frac{q}{ɛ_{0}} [∴ \int d S = 4 π r^{2}]$
$\Rightarrow E = \frac{q}{4 π r^{2} ɛ_{0}} \Rightarrow E = \frac{1}{4 π ɛ_{0}} . \frac{q}{r^{2}}$ .
From definition of electric field intensity $E = \frac{F}{q_{0}}$
$\Rightarrow \frac{F}{q_{0}} = \frac{1}{4 π ɛ_{0}} . \frac{q}{r_{2}} \Rightarrow F = \frac{1}{4 π ɛ_{0}} .$ . This is Coulomb.s law.
Expression for electric field when sheet is thick:
In case of a sheet, with finite thickness, both sides of the sheet are to be considered.
$∴$ from equation (i), we get
$\oint \to E . - \to d S = \frac{2 σ S}{ɛ_{0}}$
$or 2 E S = \frac{2 σ S}{ɛ_{0}}$
$or E = \frac{σ}{ɛ_{0}} ... ... (v)$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Similar Questions

Knowledge Check

Question 1 - Select One
What is the nature of Gaussian surface involved in Gauss's law of electrostatics?
AScalar
BElectrical
CMagnetic
DVector

Recommended Questions

Home
Ask Doubt
Profile