A series circuit contains L, C and R as circuit elements. Discuss current - voltage relation when a.c. is passed through such circuit and hence find the expression for the impedances of the circuit and resonant frequency of the circuit

Text Solution

Verified by Experts

Let a resistance R, an inductor L, a capacitor C be connected in series to a source of e.m.f. V as shown in following figure
We know that ,
(i) In a resistor, current and voltage are in phase The potential difference across resistor is
$v_{r m s} = i_{m} R$ . . . (i) (ii) In an inductor, voltage leads current by phase $π / 2$ . The potential difference across inductor is
$v_{L m} = i_{m} X_{L}$ . . . (ii)
Where $X_{L}$ is inducitive reactance
(iii) In a capacitor , voltage lage current by phase $π / 2$ . The potential differences across capacitor is
$v_{C M} = i_{m} X_{C}$ . . . (ii)
Where $X_{C}$ is capacitive reactance . The phasor diagram is shown in figure
In diagram OA , OB and OD re[resemts $v_{r m s}, v_{L m} and v_{C m}$ respectively

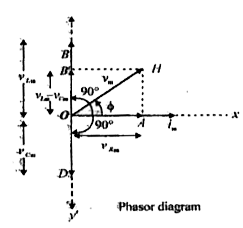
$O H = \sqrt{{(O A)}^{2} + {(O B)}^{2}}$
or $v_{m} = \sqrt{v_{r m}^{2} + (v_{l . m} 0 v_{C m}^{2})}$ . . . (iv)
Using equaitons (i) , (ii) and (iii) , then equation (iv) becomes
$v_{m} = \sqrt{i_{m}^{2} + {(i_{m} X_{1} - i_{m} X_{C})}_{m}^{2}} = i_{m} \sqrt{R^{2} + {(X_{L} - X_{C})}_{L}^{2}}$
or $\frac{v_{m}}{i_{m}} = Z where Z = \sqrt{R^{2} + {(X_{1} - X_{C})}_{1}^{2}}$
i.e. Total oppositivon of LCR circuit and is called impedance of circuit . A.t resonance $X_{L} = X_{C}, Z = R$
Expression for resonance frequency $(v_{0})$ : The freqiemcu at which LCR circuit allows for electric resonance $X_{L} = X_{C}$
or $L ω = \frac{l}{ω C} or ω^{2} = \frac{l}{L C} or ω = \frac{1}{\sqrt{L C}} or 2 π v_{0} \frac{1}{\sqrt{L C}}$
or $v_{0} = \frac{l}{2 π \sqrt{L C}}$
Difference between ohmic resistances and impedance :
Ohmic resistance of an a.c. circuit offered by a conductor connected in the circit and it is due to the nature of the material (resistivity) of the conductor . Whereas, impedance is the total opposition to the flow of a.c. by ohmic resistance, inductor and capacitor i.e.
Impedance $= \sqrt{{(X_{C} + X_{L})}_{C}^{2} + R^{2}}$

Updated on:21/07/2023