When the help of a phase diagram obtain a relation for impedance in an a.c. LCR series circuit. What is meant by resonance of this circuit ?

Text Solution

Verified by Experts

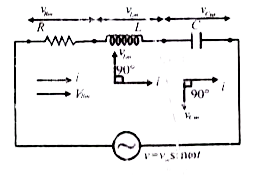
Let a resistance R, an inductor L, a capacitor C be connected in series to a source of e.m.f. V as shown in following figure
We know that ,
(i) In a resistor, current and voltage are in phase The potential difference across resistor is
$v_{r m s} = i_{m} R$ . . . (i) (ii) In an inductor, voltage leads current by phase $π / 2$ . The potential difference across inductor is
$v_{L m} = i_{m} X_{L}$ . . . (ii)
Where $X_{L}$ is inducitive reactance
(iii) In a capacitor , voltage lage current by phase $π / 2$ . The potential differences across capacitor is
$v_{C M} = i_{m} X_{C}$ . . . (ii)
Where $X_{C}$ is capacitive reactance . The phasor diagram is shown in figure
In diagram OA , OB and OD re[resemts $v_{r m s}, v_{L m} and v_{C m}$ respectively

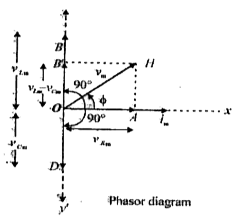
$O H = \sqrt{{(O A)}^{2} + {(O B)}^{2}}$
or $v_{m} = \sqrt{v_{r m}^{2} + (v_{l . m} 0 v_{C m}^{2})}$ . . . (iv)
Using equaitons (i) , (ii) and (iii) , then equation (iv) becomes
$v_{m} = \sqrt{i_{m}^{2} + {(i_{m} X_{1} - i_{m} X_{C})}_{m}^{2}} = i_{m} \sqrt{R^{2} + {(X_{L} - X_{C})}_{L}^{2}}$
or $\frac{v_{m}}{i_{m}} = Z where Z = \sqrt{R^{2} + {(X_{1} - X_{C})}_{1}^{2}}$
i.e. Total oppositivon of LCR circuit and is called impedance of circuit . A.t resonance $X_{L} = X_{C}, Z = R$
Expression for resonance frequency $(v_{0})$ : The freqiemcu at which LCR circuit allows for electric resonance $X_{L} = X_{C}$
or $L ω = \frac{l}{ω C} or ω^{2} = \frac{l}{L C} or ω = \frac{1}{\sqrt{L C}} or 2 π v_{0} \frac{1}{\sqrt{L C}}$
or $v_{0} = \frac{l}{2 π \sqrt{L C}}$
Difference between ohmic resistances and impedance :
Ohmic resistance of an a.c. circuit offered by a conductor connected in the circit and it is due to the nature of the material (resistivity) of the conductor . Whereas, impedance is the total opposition to the flow of a.c. by ohmic resistance, inductor and capacitor i.e.
Impedance $= \sqrt{{(X_{C} + X_{L})}_{C}^{2} + R^{2}}$

Updated on:21/07/2023