∠ACB is an angle in the semicircle of diameter AB = 5 and AC : BC = 3:4. The area of the triangle ABC is
6√2 sq. cm
4 sq. cm
12 sq. cm
6 sq. cm
The correct Answer is:D
To find the area of triangle ABC where angle ACB is inscribed in a semicircle with diameter AB = 5 and the ratio of sides AC to BC is 3:4, we can follow these steps:
Step 1: Understand the Geometry
Since AB is the diameter of the semicircle, angle ACB is a right angle (90 degrees) according to the inscribed angle theorem.
Step 2: Assign Lengths Based on the Ratio
Given that the ratio of AC to BC is 3:4, we can assign:
- AC = 3x
- BC = 4x
Step 3: Use the Pythagorean Theorem
In right triangle ACB, we can apply the Pythagorean theorem:
AB2=AC2+BC2
Substituting the known values:
52=(3x)2+(4x)2
This simplifies to:
25=9x2+16x2
25=25x2
Step 4: Solve for x
Dividing both sides by 25:
1=x2
Taking the square root:
x=1
Step 5: Find the Lengths of AC and BC
Now substituting x back into our expressions for AC and BC:
- AC = 3x = 3(1) = 3
- BC = 4x = 4(1) = 4
Step 6: Calculate the Area of Triangle ABC
The area A of triangle ABC can be calculated using the formula:
A=12×Base×Height
Here, we can take AC as the base and BC as the height:
A=12×4×3
A=12×12=6
Thus, the area of triangle ABC is 6 square units.
Final Answer
The area of triangle ABC is 6cm2.
---
Since AB is the diameter of the semicircle, angle ACB is a right angle (90 degrees) according to the inscribed angle theorem.
Given that the ratio of AC to BC is 3:4, we can assign:
- AC = 3x
- BC = 4x
In right triangle ACB, we can apply the Pythagorean theorem:
AB2=AC2+BC2
Substituting the known values:
52=(3x)2+(4x)2
This simplifies to:
25=9x2+16x2
25=25x2
Dividing both sides by 25:
1=x2
Taking the square root:
x=1
Now substituting x back into our expressions for AC and BC:
- AC = 3x = 3(1) = 3
- BC = 4x = 4(1) = 4
The area A of triangle ABC can be calculated using the formula:
A=12×Base×Height
Here, we can take AC as the base and BC as the height:
A=12×4×3
A=12×12=6
The area of triangle ABC is 6cm2.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - III21videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - IV169videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Test Yourself28videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
- BOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI15videos
MISCELLANEOUS
Similar Questions
Knowledge Check
- Question 1 - Select One
In a triangle ABC, it is known that AB=AC. Suppose D is the mid-point of AC and BD=BC=2. Then the area of the triangle ABC is-
A2B2√2C√7D2√7 - Question 2 - Select One
The side BC of ΔABC is produced to D. The bisectors of ∠ABCand∠ABD meet at E. If AB = AC and ∠BEC=24∘. then the measure of ∠ABC is :
AA)60∘BB)72∘CC)48∘DD)66∘ - Question 3 - Select One
ABC is a triangle, where BC = 2AB , ∠B = 30∘ and ∠A = 90∘. The magnitude of the side AC is
A2BC3B3BC4CBC√3D√3BC2
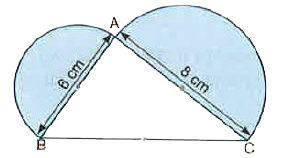
In Fig 12.58, ABC is a triangle right angled at A. Semicircles are drawn on AB and AC as diameters. Find the area of the shaded region.
 View Solution
View SolutionIn a △ABC, 2∠ABC=9∠ACB and 2∠BAC=7∠ACB. If AB = 8 cm, AC = 17 cm, then the length of BC is:
△ABC में, 2∠ABC=9∠ACB और 2∠BAC=7∠ACB| यदि AB =8 सेमी, AC =17 सेमी है, तो BC की लंबाई है:View SolutionABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
 View Solution
View SolutionIn a triangle ABC, BC = √39, AC = 5 and AB = 7. What is the measure of the angle A?
View SolutionABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
 View Solution
View Solution