In a △ABC, 2∠ABC=9∠ACB and 2∠BAC=7∠ACB. If AB = 8 cm, AC = 17 cm, then the length of BC is:
△ABC में, 2∠ABC=9∠ACB और 2∠BAC=7∠ACB| यदि AB =8 सेमी, AC =17 सेमी है, तो BC की लंबाई है:
a)8
b)25
c)15
d)9
To solve the problem step by step, we will follow the relationships given between the angles in triangle ABC and apply the properties of triangles.
Step 1: Establish the relationships between the angles
We are given:
1. 2∠ABC=9∠ACB
2. 2∠BAC=7∠ACB
Let:
- ∠ABC=B
- ∠ACB=C
- ∠BAC=A
From the first equation:
2B=9C
This implies:
BC=92
From the second equation:
2A=7C
This implies:
AC=72
Step 2: Express all angles in terms of C
Let C=2x (to keep the ratios simple).
Then:
- B=92C=92(2x)=9x
- A=72C=72(2x)=7x
Step 3: Set up the equation for the angles of the triangle
The sum of angles in a triangle is 180∘:
A+B+C=180∘
Substituting the expressions we found:
7x+9x+2x=180∘
This simplifies to:
18x=180∘
Thus:
x=10∘
Step 4: Calculate the angles
Now we can find the angles:
- C=2x=2(10)=20∘
- B=9x=9(10)=90∘
- A=7x=7(10)=70∘
Step 5: Identify the type of triangle
Since B=90∘, triangle ABC is a right triangle with:
- AB=8cm (adjacent to angle B)
- AC=17cm (hypotenuse)
Step 6: Use the Pythagorean theorem to find BC
According to the Pythagorean theorem:
AC2=AB2+BC2
Substituting the known values:
172=82+BC2
Calculating the squares:
289=64+BC2
Now, isolate BC2:
BC2=289−64
BC2=225
Taking the square root:
BC=√225=15cm
Final Answer
The length of BC is 15cm.
---
We are given:
1. 2∠ABC=9∠ACB
2. 2∠BAC=7∠ACB
- ∠ABC=B
- ∠ACB=C
- ∠BAC=A
2B=9C
This implies:
BC=92
2A=7C
This implies:
AC=72
Let C=2x (to keep the ratios simple).
Then:
- B=92C=92(2x)=9x
- A=72C=72(2x)=7x
The sum of angles in a triangle is 180∘:
A+B+C=180∘
Substituting the expressions we found:
7x+9x+2x=180∘
This simplifies to:
18x=180∘
Thus:
x=10∘
Now we can find the angles:
- C=2x=2(10)=20∘
- B=9x=9(10)=90∘
- A=7x=7(10)=70∘
Since B=90∘, triangle ABC is a right triangle with:
- AB=8cm (adjacent to angle B)
- AC=17cm (hypotenuse)
According to the Pythagorean theorem:
AC2=AB2+BC2
Substituting the known values:
172=82+BC2
Calculating the squares:
289=64+BC2
Now, isolate BC2:
BC2=289−64
BC2=225
Taking the square root:
BC=√225=15cm
The length of BC is 15cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two boys start running at the same time in the same direction at a speed of 10 km/hr and 12 km/hr respectively. In what time they will be 8 km apart?
A6 hoursB5 hoursC4 hoursD3 hours△ABC is right-angled at A. If AB = 24 cm and AC = 7 cm, then BC = ?
A31 cmB17 cmC25 cmD28 cm
In a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View SolutionIn a triangle aBC ,∠B=2∠C.AD and BE bisectors of ∠BACand∠ABC. If AB=CD . Find ∠BAC
View SolutionThe bisector of ∠B in △ABC meets AC at D. If AB = 10 cm, BC= 11 cm and AC = 14 cm, then the length of AD is:
△ABC में ∠B का समद्विभाजक AC से D पर मिलता है | यदि AB =10 सेमी, BC = 11 सेमी और AC =14 सेमी है, तो AD की लंबाई क्या होगी ?
View SolutionIn a △ABC, D is a point on side BC such that ∠ADC=∠BAC. If CA = 12 cm, CB = 8cm, then CD is equal to: △ABC में , D, भुजा BC पर एक बिंदु है इस प्रकार है कि ∠ADC=∠BAC यदि CA = 12 सेमी, CB = 8 सेमी, तो CD बराबर है: (wrong Question)
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
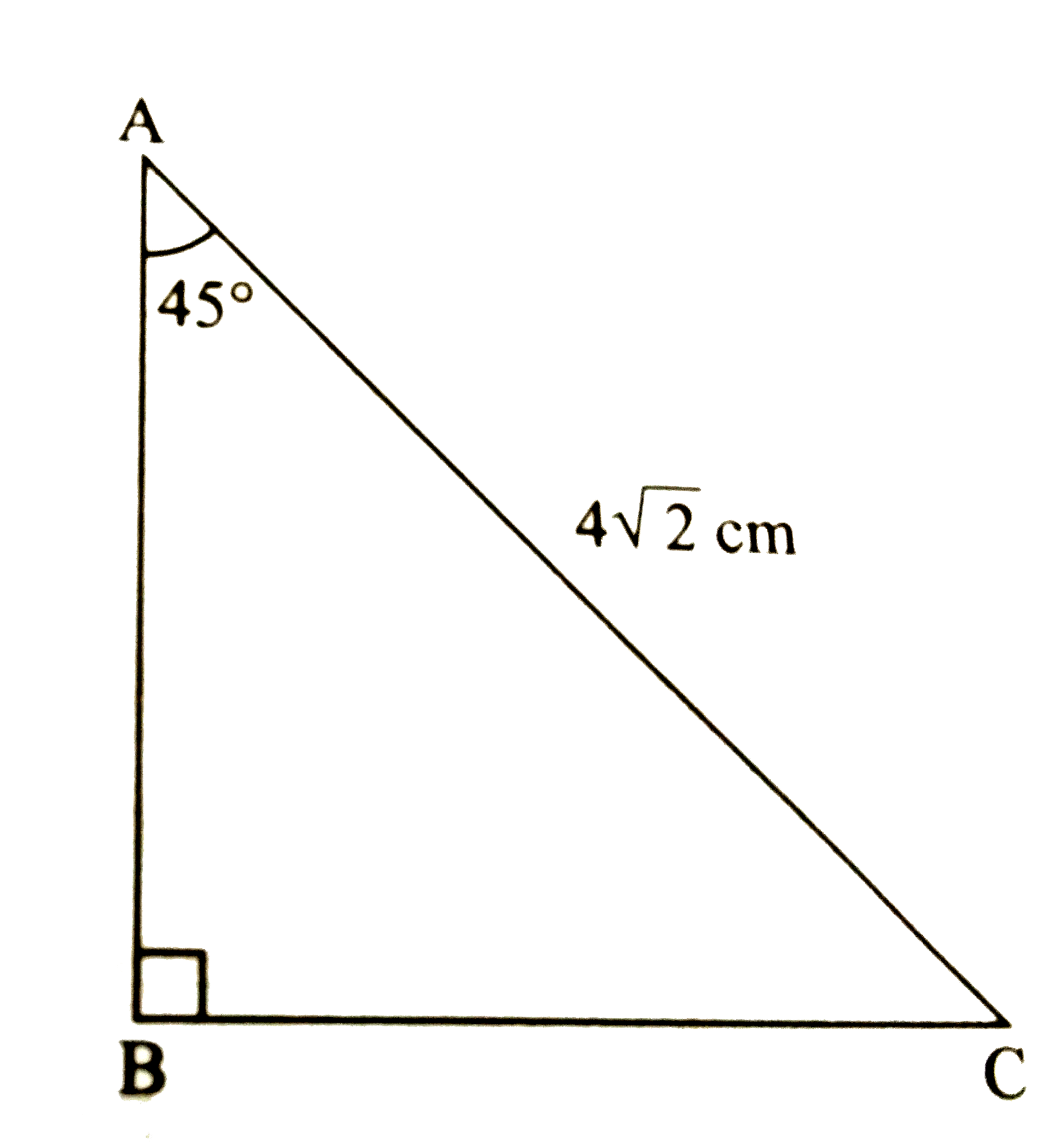
View SolutionIf △ABC is a right angled triangle with ∠ABC=90∘, and AC = 10 cm and BC = 8 cm, then the length of AB is:
यदि △ABC एक समकोण त्रिभुज है, ∠ABC=90∘,AC =10, BC =8 cm फिर AB की लंबाई है:
View Solution