In a rhombus ABCD, ∠A=60∘, AB = 12cm. Then the diagonal BD is
10 cm
2√3cm
6 cm
12 cm
The correct Answer is:D
To find the length of diagonal BD in rhombus ABCD, where angle A = 60° and side AB = 12 cm, we can follow these steps:
1. Understand the properties of a rhombus:
- In a rhombus, the diagonals bisect each other at right angles (90°).
- The opposite angles are equal.
2. Identify the angles:
- Given that angle A = 60°, angle B will also be 60° (since opposite angles are equal).
- Therefore, angle D = 60° and angle C = 120° (since the sum of angles in a quadrilateral is 360°).
3. Determine the angles at point O (the intersection of the diagonals):
- Since diagonals bisect each other at right angles, angle AOB = 90°.
- We can find angle AOB by splitting angle A into two equal parts: angle BAD = angle AOB = 30°.
4. Use triangle AOB:
- In triangle AOB, we know:
- AB = 12 cm (hypotenuse),
- Angle AOB = 90°,
- Angle OAB = 30°.
- We need to find OB (half of diagonal BD).
5. Apply trigonometric ratios:
- Using the sine function:
sin(30°)=OBAB
- We know that sin(30°)=12. Therefore:
12=OB12
- Solving for OB:
OB=12×12=6 cm
6. Calculate diagonal BD:
- Since O is the midpoint of diagonal BD, we have:
BD=2×OB=2×6=12 cm
Final Answer:
The length of diagonal BD is 12 cm.
---
- In a rhombus, the diagonals bisect each other at right angles (90°).
- The opposite angles are equal.
- Given that angle A = 60°, angle B will also be 60° (since opposite angles are equal).
- Therefore, angle D = 60° and angle C = 120° (since the sum of angles in a quadrilateral is 360°).
- Since diagonals bisect each other at right angles, angle AOB = 90°.
- We can find angle AOB by splitting angle A into two equal parts: angle BAD = angle AOB = 30°.
- In triangle AOB, we know:
- AB = 12 cm (hypotenuse),
- Angle AOB = 90°,
- Angle OAB = 30°.
- We need to find OB (half of diagonal BD).
- Using the sine function:
sin(30°)=OBAB
- We know that sin(30°)=12. Therefore:
12=OB12
- Solving for OB:
OB=12×12=6 cm
- Since O is the midpoint of diagonal BD, we have:
BD=2×OB=2×6=12 cm
The length of diagonal BD is 12 cm.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - III21videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - IV169videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Test Yourself28videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
- BOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI15videos
MISCELLANEOUS
Similar Questions
How many tiles, each 4 decimetre square, will be required to cover the floor of a room 8m long and 6m broad ?
01:36View SolutionA cistern 6 m long and 4 m wide, contains water up to a depth of 1m 25 cm. The total area of the wet surface is
03:04View SolutionABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
02:15View SolutionFind the HCF of 513, 1134 and 1215
02:57View SolutionIf a machine consumes k5 kilowatts of power every t hours, how much power in kilowatts, will three such machines consume in 10 hours ?
04:55View SolutionABCD is a rhombus whose diagonals intersect at O. If AB=10cm, diagonals BD=16 cm , find the length of diagonal AC
06:59View SolutionABCD एक समचतुर्भुज हे और ∠A=60∘ और AB=12 से.मी. हे, तो विकर्ण BD=?
02:39View Solutionएक समचतुर्भुज ABCD मे, <B=60∘ और AB = 14 सेमी है | तो विकर्ण AC होगा |
07:34View SolutionABCD एक समचतुर्भुर्ज है । सिद्ध कीजिए की विकर्ण AC,∠A व ∠C को तथा विकर्ण BD,∠B व ∠D को समद्विभजाक करते है ।
03:06View SolutionThe length of AB of the rhombus ABCD is 4 cm and if ∠BCD=60∘ then find the length of the diagonal BD.
05:45View SolutionABCD is a rhombus Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
04:18View SolutionConstruct a rhombus ABCD, when :
Diagonal AC=6.3cm and diagonal BD=5.8cm.02:40View SolutionIn rhombus ABCD , diagonal AC = 18 cm , the angle between diagonal BD and side AB is α such that cosα=0.8. Find the diagonal BD and the perimeter of rhombus ABCD.
03:12View SolutionThe diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
04:14View Solutionfind the lengths of diagonals of a rhombus AC and BD .given AB=60 cm and angle BAD=60 degree .
05:37View SolutionIn a rhombus ABCD, length of each side is 10 cm and ∠A=60∘. Find the lengths of its diagonals AC and BD.
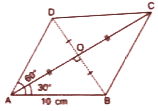 06:29View Solution
06:29View Solution

