The centroid of a triangle ΔABC is G. If the area of ΔABC=72 sq. units, then the area of ΔBGC is
16 sq. units
24 sq. units
36 sq. units
48 sq. units
The correct Answer is:B
To find the area of triangle BGC given that the area of triangle ABC is 72 square units, we can follow these steps:
1. Understanding the Centroid: The centroid (G) of a triangle divides it into six smaller triangles of equal area. This is a key property of centroids in triangles.
2. Total Area of Triangle ABC: We know that the total area of triangle ABC is given as 72 square units.
3. Dividing the Area: Since the centroid divides the triangle into six equal areas, we can denote the area of each of these smaller triangles as x. Therefore, the total area of triangle ABC can be expressed as:
Area of ΔABC=6x
Given that the area is 72 square units, we have:
6x=72
4. Calculating x: To find x, we divide both sides of the equation by 6:
x=726=12
5. Finding the Area of Triangle BGC: The area of triangle BGC consists of two of these smaller triangles (BGA and BGC). Therefore, the area of triangle BGC can be expressed as:
Area of ΔBGC=2x
Substituting the value of x:
Area of ΔBGC=2×12=24 square units
6. Final Answer: Thus, the area of triangle BGC is 24 square units.
Summary:
The area of triangle BGC is 24 square units.
Area of ΔABC=6x
Given that the area is 72 square units, we have:
6x=72
x=726=12
Area of ΔBGC=2x
Substituting the value of x:
Area of ΔBGC=2×12=24 square units
The area of triangle BGC is 24 square units.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - III21videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - IV169videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Test Yourself28videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
- BOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI15videos
MISCELLANEOUS
Similar Questions
Knowledge Check
- Question 1 - Select One
The medians of a triangle ABC meet at G. If the area of the triangle be 120 sq cm, then the area of the triangle GBC is
A30 sq.cmB50 sq. cmC20 sq.cmD40 sq.cm - Question 2 - Select One
Three medians AD, BE and CF of ΔABC intersect at G. The area of ΔABC is 36 sq. cm. Then the area of ΔCGE is
A12 sq. cmB6 sq. cmC9 sq. cmD18 sq. cm - Question 3 - Select One
Two triangles ABC & PQR are congruent. If the area of Δ ABC is 60 sq. cm, then area of ΔPQR will be
A60 sq. cmB30 sq. cmC15 sq. cmD120 sq. cm
If G is the centriod of ΔABC and if area of ΔAGB is 5 sq units.Then area of ΔABC is P sq units then value of P is
View SolutionThe centroid of a triangle ABC is G. The area of triangle ABC is 60 cm2. The area of triangle GBC is.
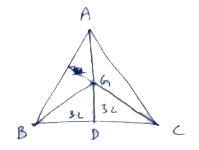
View SolutionIn a ΔABC,AD is median, G is a Mid point of AD. If area of ΔAGC IS 32 SQ . units then find area of ΔBGC
 View Solution
View SolutionG is the centroid of the triangle ABC. Prove that the area of the triangle ABG is one third of the area of the triangle ABC.
View SolutionThe three medians AD, BE and CF of ΔABC intersect at point G. If the area of ΔABC is 60 sq.cm. then the area of the quadrilateral BDGF is :
View Solution